题目内容
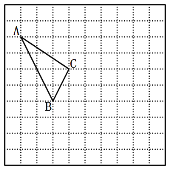
【题目】如图,已知直线l1:y=2x+1与坐标轴交于A、C两点,直线l2:y=﹣x﹣2与坐标轴交于B、D两点,两线的交点为P点,
(1)求出点P的坐标;
(2)求△APB的面积;
(3)在x轴上是否存在点Q,使得△OPQ的面积等于6,若存在,求出Q点坐标,若不存在,请说明理由.

【答案】(1)点P坐标为:(-1,-1); (2)![]() ;(3)Q点坐标为(12,0)或(-12,0)
;(3)Q点坐标为(12,0)或(-12,0)
【解析】
(1)将两直线方程联立成方程组,求解即可得到P的坐标;
(2)先求出A,B,P的坐标,根据面积公式即可求解;
(3)设Q点坐标为(a,0),根据三角形的面积公式列方程求解即可.
解:(1)∵y1=2x+1与y2=﹣x﹣2相交于点P,
∴![]() ,
,
解之得:![]() ,
,
∴点P坐标为:(-1,-1);
(2)∵直线y=2x+1交y轴于A点,
∴A(0,1)即OA=1,
又∵直线y=-x-2交y轴于B点,
∴B(0,-2)即OB=2 ,
∴AB=3 ,
∴![]() ;
;
(3) x轴上存在Q点使得△OPQ的面积为6,
设Q点坐标为(a,0),
∴![]() ,
,
解之得:a=12或a=-12,
∴Q点坐标为(12,0)或(-12,0).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目