Question

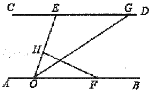
【题目】如图，在平行四边形中，当底边上的高由小到大变化时，平行四边形的面积也随之发生变化，我们得到如下数据：

底边AB上的高x（cm）	2	3	4	5
平行四边形ABCD的面积y(cm2)	12	18	24	30

（1）在这个变化过程中，自变量、因变量分别是什么？

（2）与之间的关系式可以表示为 ；

（3）由表格中的数据可以发现，当每增加时，如何变化？

（4）若平行四边形的面积为，此时底边上的高为多少？

Answer 1

【答案】（1）底边上的高为自变量，平行四边形的面积为因变量；（2）；（3）增加；（4）底边上的高为.

【解析】

（1）平行四边形的面积随高的变化而变化，底边上的高是自变量，平行四边形的面积是因变量．
（2）根据平行四边形的面积公式就可以得到．
（3）根据图表就可以得到当x每增加1cm时，y的变化．
（4）代入函数关系式，即可求出此时底边上的高的值.

（1）在这个变化过程中，底边上的高为自变量，平行四边形的面积为因变量.

（2）与之间的关系式可以表示为：

（3）由表格中的数据可以发现，当每增加时，增加

（4）当时，，

解得.

此时底边上的高为.