题目内容

已知：关于x的方程mx²-3（m-1）x+2m-3=0．
（1）当m取何整数值时，关于x的方程mx²-3（m-1）x+2m-3=0的根都是整数；
（2）若抛物线y=mx²-3（m-1）x+2m-3向左平移一个单位后，过反比例函数y= $数学公式$ （k≠0）上的一点（-1，3），
①求抛物线y=mx²-3（m-1）x+2m-3的解析式；
②利用函数图象求不等式 $数学公式$ -kx＞0的解集．

解：（1）当m=0时，x=1；
当m≠0，可解得x₁=1，x₂= 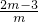$\text{[math]}$ =2- $\text{[math]}$ ；
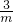∴m=±1、±3时，x均有整数根；
综上可得m=0、±1、±3时，x均有整数根．

（2）①抛物线向左平移一个单位后得到y=m（x+1）²-3（m-1）（x+1）+2m-3，过点（-1，3），代入解得：m=3；
∴抛物线解析式为y=3x²-6x+3．
②∵反比例函数y= $\text{[math]}$ （k≠0）经过点（-1，3），
∴k=-1×3=-3；
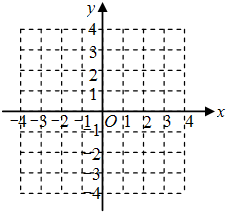
作出y=kx、y= $\text{[math]}$ （k≠0）的图象（如右图）
由图可知：当x＞1或-1＜x＜0时， $\text{[math]}$ ＞kx；
即：不等式 $\text{[math]}$ -kx＞0的解集为：x＞1或-1＜x＜0．
分析：（1）原方程可能是一元一次方程也可能是一元二次方程，因此分m=0和m≠0两种情况，先求出两种情况下方程的根，再由根是整数确m定的值．
（2）①先表示出平移后的抛物线解析式，然后将点（-1，3）代入其中求解即可；
②根据反比例函数过（-1，3）确定k的值，然后分别作出y= $\text{[math]}$ 和y=kx的函数图象，找出前者的图象在后者上方的部分即可．
点评：该题涉及到：方程与函数的联系、函数解析式的确定以及利用图象法解不等式的方法等知识．考查的内容较为基础，难度不大．