题目内容
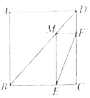
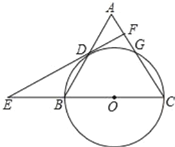
【题目】如图,在![]() ABC中,CA=CB=10,AB=12,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.则下列结论正确的是_____
ABC中,CA=CB=10,AB=12,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.则下列结论正确的是_____
①DF⊥AC; ②DO=DB; ③S△ABC=48; ④cos∠E=![]() .
.
【答案】①③④
【解析】
连接OD,BG,CD,如图,利用切线的性质得到OD⊥DF,再利用圆周角定理和等腰三角形的性质证明OD∥AC,则可对①进行判断;利用OB=![]() BC=5,BD=6可对②进行判断;利用勾股定理计算出CD=8,则可计算出
BC=5,BD=6可对②进行判断;利用勾股定理计算出CD=8,则可计算出![]() ABC的面积,从而可对③进行判断;利用面积法计算出BG=
ABC的面积,从而可对③进行判断;利用面积法计算出BG=![]() ,则cos∠CBG=
,则cos∠CBG=![]() ,然后证明∠E=∠CBG,从而可对④进行判断.
,然后证明∠E=∠CBG,从而可对④进行判断.
解:连接OD,BG,CD,如图,
∵DF为切线,
∴OD⊥DF,
∵BC为直径,
∴∠BDC=90°,
∵CA=CB,
∴CD平分AB,即AD=BD=6,
而OB=OC,
∴OD为![]() ABC的中位线,
ABC的中位线,
∴OD∥AC,
∴DF⊥AC,所以①正确;
∵OB=![]() BC=5,BD=6,
BC=5,BD=6,
∴OD≠BD,所以②错误;
在Rt![]() BCD中,CD=
BCD中,CD=![]() =8,
=8,
∴S△ABC=![]() CDAB=
CDAB=![]() ×8×12=48,所以③正确;
×8×12=48,所以③正确;
∵BC为直径,
∴∠BGC=90°,
∴S△ABC=![]() BGAC=48,
BGAC=48,
∴BG=![]() ,
,
∴cos∠CBG=![]() =
=![]() =
=![]() ,
,
∵BG⊥AC,EF⊥AC,
∴BG∥EF,
∴∠E=∠CBG,
∴cos∠E=![]() ,所以④正确.
,所以④正确.
故答案为:①③④.


 阅读快车系列答案
阅读快车系列答案【题目】某校兴趣小组以问卷调查的形式,随机调查了某地居民对武汉封城后续措施的了解情况,设置了多选题,并将调查结果绘制成如图不完整的统计图.
选项 | A | B | C | D | E |
后续措施 | 扩大宣传力度 | 分类隔离病人 | 封闭小区 | 聘请专业物资 | 采取其他措施 |
选择人次 | 25 | 85 | 15 | 35 |

已知平均每人恰好选择了两个选项,根据以上信息回答下列问题:
(1)求参与本次问卷调查的居民人数,并补全条形统计图;
(2)在扇形统计图中,求E选项对应圆心角α的度数;
(3)根据此次调查结果估计该地100万居民当中选择D选项的人数.