题目内容
【题目】在平面直角坐标系中，点
在抛物线上，将抛物线
在点
右侧的部分沿着直线
翻折，翻折后的图象与原抛物线剩余部分合称为图象
．
（1）当
时，
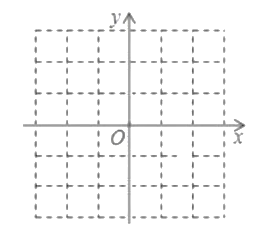
①在如图的平面直角坐标系中画出图象；
②直接写出图象对应函数的表达式；
③当
时，图象对应函数的最小值为
求
的取值范围．
（2）当
时，直接写出图象对应函数
随
增大而减小时的取值范围．
（3）若图象上有且只有三个点到直线
的距离为
，直接写出
的值．
【答案】（1）①作图见解析；②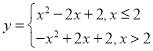
；③
；（2）
或
；（3）
【解析】
（1）①先画出翻折之前的抛物线，再把
的部分沿着直线
翻折即可；
②翻折之后的图象形状不变，开口向下，再利用待定系数法即可解决问题；
（2）画出当
时的图象G，根据图象分析即可；
（3）利用数形结合的思想，画出图象，分类讨论即可．
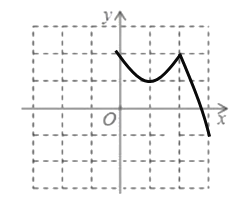
（1）①当
时，抛物线解析式为：
，则
，因此翻折后的图象如图：
②当时为解析式为，
沿翻折之后，开口向下，形状不变，故设翻折之后的解析式为：
，将点
，
代入可得：
，解得
，
∴当时，
，故图象
对应函数的表达式为：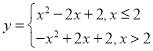
③把
代入得
，
∵
，
；
（2）当时，原函数的顶点坐标为
，故图象G如图：
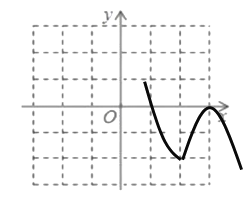
根据图象可知
随
增大而减小时的取值范围为：或；
（3）点
在抛物线
上，故
，翻折之前的顶点坐标为
，翻折之后的解析式为
，翻折之后的顶点坐标为
，
①当点A在对称轴右侧时，即
时：
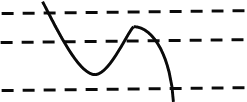
若直线在点A上方，则只需让点A到直线的距离为3即可，即
，解得：
（舍）；
若直线
在点A下方，且在翻折前顶点的上方，则需让的顶点和点A到直线的距离一个刚好等于3，一个小于3即可，即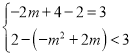
或
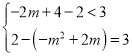，解得：
；
若直线在翻折前顶点的下方，则只需让翻折前顶点到直线的距离 3即可，即
，此时无解；
②当点A在对称轴左侧时，即
时：
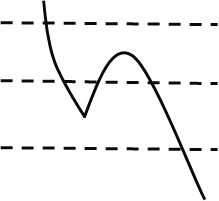
若直线在翻折后顶点的上方，则只需让翻折后顶点到直线的距离 3即可，即
，解得
（舍）；
若直线在点A上方，且在翻折后顶点的下方，则需让的顶点和点A到直线的距离一个刚好等于3，一个小于3即可，即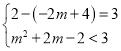
或
，解得：；
若直线在点A下方，则只需让点A到直线的距离为3即可，此时
；
综上所述，m的值为：．
