Question

【题目】如图，在△ABC中，∠ABC=∠ACB，以AC为直径的⊙O分别交AB、BC于点M、N，点P在AB的延长线上，且∠CAB=2∠BCP．

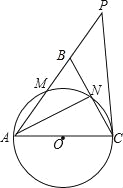
（1）求证：直线CP是⊙O的切线；

（2）若BC=2，sin∠BCP=，求点B到AC的距离．

Answer 1

【答案】(1)证明见解析；（2）4.

【解析】

试题分析：（1）利用直径所对的圆周角为直角，2∠CAN=∠CAB，∠CAB=2∠BCP判断出∠ACP=90°即可；

（2）利用锐角三角函数，即勾股定理即可．

试题解析：（1）∵∠ABC=∠ACB，

∴AB=AC，

∵AC为⊙O的直径，

∴∠ANC=90°，

∴∠CAN+∠ACN=90°，2∠BAN=2∠CAN=∠CAB，

∵∠CAB=2∠BCP，

∴∠BCP=∠CAN，

∴∠ACP=∠ACN+∠BCP=∠ACN+∠CAN=90°，

∵点D在⊙O上，

∴直线CP是⊙O的切线；

（2）如图，作BF⊥AC

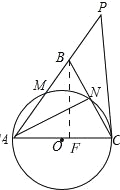
∵AB=AC，∠ANC=90°，

∴CN=CB=，

∵∠BCP=∠CAN，sin∠BCP=，

∴sin∠CAN=，

∴

∴AC=5，

∴AB=AC=5，

设AF=x，则CF=5﹣x，

在Rt△ABF中，BF2=AB2﹣AF2=25﹣x2，

在Rt△CBF中，BF2=BC2﹣CF2=2O﹣（5﹣x）2，

∴25﹣x2=2O﹣（5﹣x）2，

∴x=3，

∴BF2=25﹣32=16，

∴BF=4，

即点B到AC的距离为4．