题目内容
【题目】如图,已知直线AB//CD,直线EF和直线AB,CD分别交于点B和点D,在直线 EF 上有一动点P.
(1).P点在线段BD上(点P 与点B,D不重合),请证明 :∠PAB+∠PCD=∠APC;
(2).若点P不在线段BD 上,请写出∠PAB, ∠PCD, ∠APC之间的数量关系,并画出相关图形,说明理由.
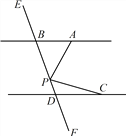
【答案】(1)证明见解析;(2)当P点在射线BE上时,![]() ;当P点在射线DF 上时,
;当P点在射线DF 上时,![]() ,画图及证明见解析.
,画图及证明见解析.
【解析】试题分析:(1)过点P作PQ∥AB,根据平行公理求出PQ∥CD,再根据两直线平行,内错角相等可得∠APQ=∠PAB,∠CPQ=∠PCD,再根据∠APC=∠APQ+∠CPQ等量代换即可得证;(2)分点P在线段BD 的延长线上和点P在线段DB 的延长线上两种情况讨论∠PAB,∠PCD,∠APC之间的数量关系,过点P作PQ∥AB,然后根据类比(1)的方法探究证明即可.
试题解析:
(1) 过点P作PQ//AB .
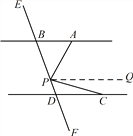
![]() ,
, ![]() .
.
![]() ,
,![]() ,
,
![]() .
.
(2) Ⅰ.如图,当P点在射线BE上时.
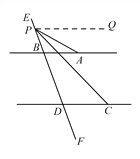
过点P作PQ//AB .
![]() ,
, ![]() .
.
![]() ,
,![]() ,
,
![]() .
.
Ⅱ.如图,当P点在射线DF 上时,
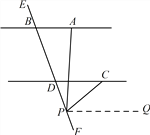
过点P作PQ//AB .
![]() ,
, ![]() .
.
![]()
![]() ,
, ![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目