题目内容
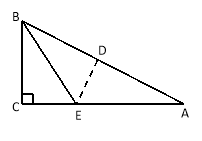
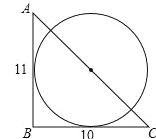
【题目】如图,△ABC中,∠B=90°,AB=11,BC=10,若⊙O的半径为5且与AB、BC相切,以下说法不正确的是 .
①圆心O是∠B的角平分线与AC的交点;
②圆心O是∠B的角平分线与AB的垂直平分线的交点;
③圆心O是AB的垂直平分线与BC的垂直平分线的交点;
④圆心O是∠B的角平分线与BC的垂直平分线的交点.
【答案】①②③
【解析】
试题分析:首先连接OD,OE,
∵⊙O的半径为5且与AB、BC相切,
∴OD⊥AB,OE⊥BC,OD=OE=5,
∵∠B=90°,
∴四边形ODBE是正方形,
∴BE=BD=OE=OD=5,
∴点O在∠B的平分线上,CE=BC﹣BE=5,AD=AB﹣BD=11﹣5=6,
∴OE是BC的垂直平分线,OD不是AB的垂直平分线,
∵OA=![]() ,OC=
,OC=![]() ,
,
∴OA≠OC,
即O不在AC的垂直平分线上;
∵AC=![]() ,
,
∴点O不在AC上.
∴①②③错误,④正确.
故答案为:①②③.


练习册系列答案
相关题目