��Ŀ����
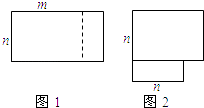
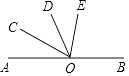
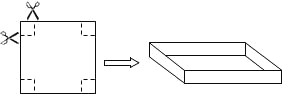
����Ŀ����һ�ű߳�Ϊ40cm��������Ӳֽ����вü����۳�һ����������ӣ�ֽ��ĺ�Ⱥ��Բ��ƣ�����ͼ������������Ӳֽ����ĽǸ�����һ��ͬ����С�������Σ���ʣ�ಿ���۳�һ���ǵij�������ӣ�
��1���������������εı߳�Ϊ9cmʱ����������ӵĵ���߳�Ϊ cm����Ϊ cm��
��2��Ҫʹ�۳ɵij�������ӵĵ����Ϊ484cm2����ô�����������α߳�Ϊ���٣�
��3���۳ɵij�������ӵIJ�����Ƿ������ֵ������У����������ֵ�ʹ�ʱ�����������εı߳������û�У�˵�����ɣ�
���𰸡�(1)��22��9��(2)��9cm��(3)����x=10ʱ��y���=800
��������
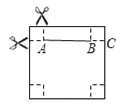
���������(1)����ͼ�������������εı߳�Ϊ9cm����BC=9cm����������ӵĵ���߳�����AB�ij������������α߳�������ɣ�(2)��������������εı߳�Ϊx cm����AB=��40��2x��cm�����ݺ��ӵĵ����Ϊ484cm2���з��̽�����ɣ�(3)��������������εı߳�Ϊx cm�����ӵIJ����Ϊy cm2�������=4���������������y=��8x2+160x���䷽����ֵ��
���������(1)����ͼ��ʾ�� ����֪�ã�BC=9cm��AB=40��2��9=22cm��
(2)��������������εı߳�Ϊx cm�� ��40��2x��2=484�� ��40��2x=��22��
���x1=31���������⣬��ȥ����x2=9��
(3)���۳ɵij�������ӵIJ���������ֵ�� ������������εı߳�Ϊx cm�����ӵIJ����Ϊy cm2����y��x�ĺ�����ϵʽΪy=4��40��2x��x�� ��y=��8x2+160x�� y=��8��x��10��2+800��
�ߩ�8��0�� ��y�����ֵ�� ����x=10ʱ��y���=800��

 ��У����ϵ�д�
��У����ϵ�д�