题目内容
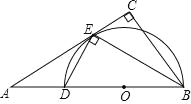
【题目】在三角形纸片ABC中,∠C=90°,∠A=30°,AC=3,折叠该纸片,如图,使点A和点B重合,折痕与AB、AC分别相交于点D和点E,折痕DE的长为
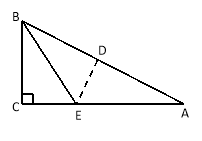
【答案】1
【解析】先根据,∠C=90°,∠A=30°,AC=3求出AB的长,再根据图形翻折变换的性质可知DE⊥AB,AE=BE=![]() AB,再在Rt△ADE中,由DE=AEtan∠A即可得出DE的长.
AB,再在Rt△ADE中,由DE=AEtan∠A即可得出DE的长.
解:∵△ABC中,∠C=90°,∠A=30°,AC=3,
∴AB=![]() =
=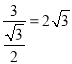 ,
,
∵△BDE是△ADE翻折而成,DE为折痕,
∴DE⊥AB,AE=BE=![]() AB=
AB=![]() ×2
×2![]() =
=![]() ,
,
在Rt△ADE中,DE=AEtan∠A=![]() ×tan30°=
×tan30°=![]() ×
×![]() =1.
=1.
故答案为:1.
考查的是图形翻折变换的性质及三角函数的定义,熟知“折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等”是解答此题的关键

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目