题目内容
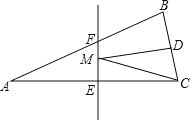
【题目】如图，抛物线
与x轴交于A，B两点，它们的对称轴与x轴交于点N，过顶点M作ME⊥y轴于点E，连结BE交MN于点F.已知点A的坐标为（﹣1，0）.
（1）求该抛物线的解析式及顶点M的坐标；
（2）求△EMF与△BNF的面积之比.
【答案】（1）
，（1，4）；（2）
.
【解析】试题分析：（1）直接将（﹣1，0）代入求出即可，再利用配方法求出顶点坐标.
（2）利用EM∥BN，则△EMF∽△BNF，进而求出△EMF与△BNE的面积之比．
试题解析：解：（1）∵点A在抛物线
上，
∴
，解得：c=3，
∴抛物线的解析式为
.
∵
，
∴抛物线的顶点M（1，4）；
（2）∵A（﹣1，0），抛物线的对称轴为直线x=1，∴点B（3，0）.
∴EM=1，BN=2.
∵EM∥BN，∴△EMF∽△BNF.∴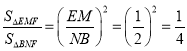
．
练习册系列答案
相关题目
【题目】数学活动课上，老师提出问题：如图，有一张长4dm，宽3dm的长方形纸板，在纸板的四个角裁去四个相同的小正方形，然后把四边折起来，做成一个无盖的盒子，问小正方形的边长为多少时，盒子的体积最大．
下面是探究过程，请补充完整：
（1）设小正方形的边长为xdm，体积为ydm3，根据长方体的体积公式得到y和x的关系式： ；
（2）确定自变量x的取值范围是 ；
（3）列出y与x的几组对应值．
x/dm | … |
|
|
|
|
|
|
| 1 |
|
| … |
y/dm3 | … | 1.3 | 2.2 | 2.7 | 3.0 | 2.8 | 2.5 | 1.5 | 0.9 | … |
（说明：表格中相关数值保留一位小数）
（4）在下面的平面直角坐标系xOy中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（5）结合画出的函数图象，解决问题：当小正方形的边长约为 dm时，盒子的体积最大，最大值约为 dm3．
