题目内容
【题目】如图，将一块含30°角的直角三角版和半圆量角器按如图的方式摆放，使斜边与半圆相切．若半径OA=4，则图中阴影部分的面积为 ． （结果保留π） 
【答案】
+2 
【解析】解：如图所示：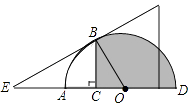 
∵斜边与半圆相切，点B是切点，
∴∠EBO=90°．
又∵∠E=30°，
∴∠EBC=60°．
∴∠BOD=120°，
∵OA=OB=4，
∴OC= 
OB=2，BC=2 ．
∴S阴影=S扇形BOD+S△BOC= 
+ ×2×2 = +2 ．
所以答案是： +2 ．
【考点精析】本题主要考查了切线的判定定理和扇形面积计算公式的相关知识点，需要掌握切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线；在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）才能正确解答此题．
练习册系列答案
名校课堂系列答案
相关题目
【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | 9.5 |
（1）完成表中填空①；②；
（2）请计算甲六次测试成绩的方差；
（3）若乙六次测试成绩方差为 
，你认为推荐谁参加比赛更合适，请说明理由．
