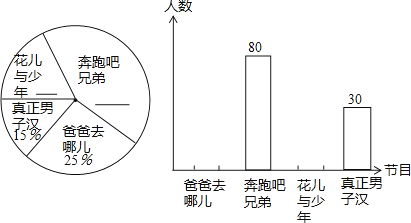
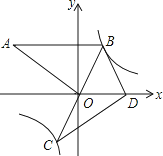
��Ŀ����
����Ŀ������ABCD�У������Խ���AC��BD�ཻ�ڵ�O����MON+��BCD=180�㣬��MON�Ƶ�O��ת������OM����BC�ڵ�E������ON����DC�ڵ�F������EF��
��1����ͼ1������ABC=90��ʱ����OEF����״����
��2����ͼ2������ABC=60��ʱ�����жϡ�OEF����״����˵�����ɣ�
��3���ڣ�1���������£�����MON�Ķ����Ƶ�AO���е�O�䴦����MO��N�Ƶ�O����ת���������MO��N+��BCD=180�㣬����O��M��ֱ��BC�ڵ�E������O��N��ֱ��CD�ڵ�F����BC=4����![]() =
=![]() ʱ��ֱ��д���߶�CE�ij���
ʱ��ֱ��д���߶�CE�ij���
���𰸡�
��1��
�⣺��OEF�ǵ���ֱ�������Σ�
֤������ͼ1��
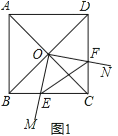
������ABCD�У���ABC=90�㣬
���ı���ABCD�������Σ�
��OB=OC����BOC=90�㣬��BCD=90�㣬��EBO=��FCO=45�㣬
���BOE+��COE=90�㣬
�ߡ�MON+��BCD=180�㣬
���MON=90�㣬
���COF+��COE=90�㣬
���BOE=��COF��
�ڡ�BOE���COF�У�
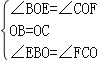 ��
��
���BOE�ա�COF��ASA����
��OE=OF��
���OEF�ǵ���ֱ�������Σ�
�ʴ�Ϊ����ֱ�������Σ�
��2��
�⣺��OEF�ǵȱ������Σ�
֤������ͼ2����O����OG��BC��G����OH��CD��H��
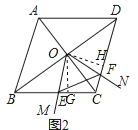
���OGE=��OGC=��OHC=90�㣬
���ı���ABCD�����Σ�
��CAƽ�֡�BCD����ABC+BCD=180�㣬
��OG=OH����BCD=180�㩁60��=120�㣬
�ߡ�GOH+��OGC+��BCD+��OHC=360�㣬
���GOH+��BCD=180�㣬
���MON+��BCD=180�㣬
���GOH=��EOF=60�㣬
�ߡ�GOH=��GOF+��FOH����EOF=��GOF+��EOG��
���EOG=��FOH��
�ڡ�EOG���FOH�У�
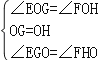 ��
��
���EOG�ա�FOH��ASA����
��OE=OF��
���OEF�ǵȱ������Σ�
��3��
֤������ͼ3��
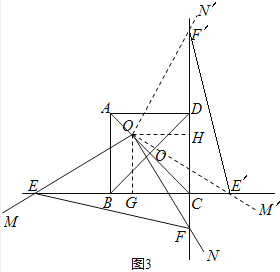
������ABCD�У���ABC=90�㣬
���ı���ABCD�������Σ�
��![]() =
=![]() ��
��
��O����O��G��BC��G����O��H��CD��H��
���O��GC=��O��HC=��BCD=90�㣬
���ı���O��GCH�Ǿ��Σ�
��O��G��AB��O��H��AD��
��![]() =
=![]() =
=![]() =
=![]() ��
��
��AB=BC=CD=AD=4��
��O��G=O��H=3��
���ı���O��GCH�������Σ�
��GC=O��G=3����GO��H=90��
�ߡ�MO��N+��BCD=180�㣬
���EO��F=90�㣬
���EO��F=��GO��H=90�㣬
�ߡ�GO��H=��GO��F+��FO��H����EO��F=��GO��F+��EO��G��
���EO��G=��FO��H��
�ڡ�EO��G���FO��H�У�
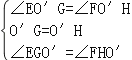 ��
��
���EO��G�ա�FO��H��ASA����
��O��E=O��F��
���O��EF�ǵ���ֱ�������Σ�
��S������ABCD=4��4=16��![]() =
=![]() ��
��
��S��O��EF=18��
��S��O��EF=![]() O��E2��
O��E2��
��O��E=6��
��RT��O��EG��EG=![]() =
=![]() =3
=3![]() ��
��
��CE=CG+EG=3+3![]() ��
��
���ݶԳ��Կ�֪������M��ON����ת����ͼ��ʾλ��ʱ��
CE��=E��G��CG=3![]() ��3��
��3��
���Ͽɵã��߶�CE�ij�Ϊ3+3![]() ��3
��3![]() ��3��
��3��
����������1��������ı���ABCD�������Σ�Ȼ����������ε����ʿɵá�EBO=��FCO=45�㣬OB=OC���ٸ���ͬ�ǵ������ȿɵá�BOE=��COF��Ȼ�����á��DZ߽ǡ�֤����BOE�͡�COFȫ�ȣ�����ȫ�������ζ�Ӧ����ȼ��ɵ�֤��
��2����O����OG��BC��G����OH��CD��H���������ε����ʿɵ�CAƽ�֡�BCD����ABC+BCD=180�㣬���OG=OH����BCD=180�㩁60��=120�㣬�Ӷ���á�GOH=��EOF=60�㣬�ٸ��ݵ����������ɵá�EOG=��FOH��Ȼ�����á��DZ߽ǡ�֤����EOG�͡�FOHȫ�ȣ�����ȫ�������ζ�Ӧ����ȼ��ɵ�֤��
��3����O����OG��BC��G����OH��CD��H��������ı���O��GCH�������Σ��Ӷ����GC=O��G=3����GO��H=90�㣬Ȼ�����á��DZ߽ǡ�֤����EO��G�͡�FO��Hȫ�ȣ�����ȫ�������ζ�Ӧ����ȼ���֤�á�O��EF�ǵ���ֱ�������Σ�������֪��õ���ֱ�������ε�ֱ�DZ�O��E�ij���Ȼ����ݹ��ɶ������EG���������CE�ij���
�����㾫����������Ĺؼ���������ȫ�������ε����ʵ����֪ʶ������ȫ�������εĶ�Ӧ�����; ȫ�������εĶ�Ӧ����ȣ��Լ��Թ��ɶ����ĸ�������⣬�˽�ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2��