题目内容
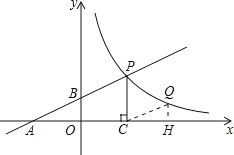
【题目】如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y= ![]() (x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求双曲线的解析式;
(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.
【答案】
(1)
解:(1)把A(﹣2,0)代入y=ax+1中,求得a= ![]() ,
,
∴y= ![]() x+1,
x+1,
由PC=2,把y=2代入y= ![]() x+1中,得x=2,即P(2,2),
x+1中,得x=2,即P(2,2),
把P代入y= ![]() 得:k=4,
得:k=4,
则双曲线解析式为y= ![]() ;
;
(2)
解:
设Q(a,b),
∵Q(a,b)在y= ![]() 上,
上,
∴b= ![]() ,
,
当△QCH∽△BAO时,可得 ![]() ,即
,即 ![]() ,
,
∴a﹣2=2b,即a﹣2= ![]() ,
,
解得:a=4或a=﹣2(舍去),
∴Q(4,1);
当△QCH∽△ABO时,可得 ![]() ,即
,即 ![]() =
= ![]() ,
,
整理得:2a﹣4= ![]() ,
,
解得:a=1+ ![]() 或a=1﹣
或a=1﹣ ![]() (舍),
(舍),
∴Q(1+ ![]() ,2
,2 ![]() ﹣2).
﹣2).
综上,Q(4,1)或Q(1+ ![]() ,2
,2 ![]() ﹣2).
﹣2).
【解析】(1)把A坐标代入直线解析式求出a的值,确定出直线解析式,把y=2代入直线解析式求出x的值,确定出P坐标,代入反比例解析式求出k的值,即可确定出双曲线解析式;(2)设Q(a,b),代入反比例解析式得到b= ![]() ,分两种情况考虑:当△QCH∽△BAO时;当△QCH∽△ABO时,由相似得比例求出a的值,进而确定出b的值,即可得出Q坐标.
,分两种情况考虑:当△QCH∽△BAO时;当△QCH∽△ABO时,由相似得比例求出a的值,进而确定出b的值,即可得出Q坐标.
【考点精析】根据题目的已知条件,利用一次函数的性质和一次函数的图象和性质的相关知识可以得到问题的答案,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.

 名校课堂系列答案
名校课堂系列答案