题目内容
【题目】如图，在平面直角坐标系中，∠AOB=90°，AB∥x轴，OB=2，双曲线y=
经过点B，将△AOB绕点B逆时针旋转，使点O的对应点D落在x轴的正半轴上．若AB的对应线段CB恰好经过点O．
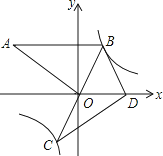
（1）求点B的坐标和双曲线的解析式；
（2）判断点C是否在双曲线上，并说明理由．
【答案】
（1）
解：∵AB∥x轴，
∴∠ABO=∠BOD，
∵∠ABO=∠CBD，
∴∠BOD=∠OBD，
∵OB=BD，
∴∠BOD=∠BDO，
∴△BOD是等边三角形，
∴∠BOD=60°，
∴B（1，
）；
∵双曲线y=
经过点B，
∴k=1×=．
∴双曲线的解析式为y=
．
（2）
解：∵∠ABO=60°，∠AOB=90°，
∴∠A=30°，
∴AB=2OB，
∵AB=BC，
∴BC=2OB，
∴OC=OB，
∴C（﹣1，
），
∵﹣1×（）=，
∴点C在双曲线上．
【解析】（1）先求得△BOD是等边三角形，即可求得B的坐标，然后根据待定系数法即可求得双曲线的解析式；
（2）求得OB=OC，即可求得C的坐标，根据C的坐标即可判定点C是否在双曲线上．
练习册系列答案
相关题目
