Question

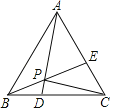
【题目】如图所示，等边△ABC的边长为4，点D是BC边上一动点，且CE＝BD，连接AD，BE，AD与BE相交于点P，连接PC．则线段PC的最小值等于_____．

Answer 1

【答案】

【解析】

由“SAS”可证△ABD△BCE，可得∠BAD＝∠CBE，由此进一步可求∠APB＝120°，据此如图，作等腰△AOB，使OA＝OB，∠AOB＝120°，连接OC，OP，可得点P在以点O为圆心，OB为半径的圆上，当点O，点P，点C共线时，PC有最小值，最后利用直角三角形的性质进一步求解即可．

∵△ABC是等边三角形，

∴AB＝AC＝BC＝4，∠ABC＝∠BAC＝∠ACB＝60°，

∵CE＝BD，∠ABC＝∠BCE＝60°，AB＝BC，

∴△ABD△BCE（SAS）

∴∠BAD＝∠CBE，

∵∠ABP+∠CBP＝∠ABC＝60°，

∴∠ABP+∠BAD＝60°，

∴∠APB＝120°，

如图：作等腰△AOB，使OA＝OB，∠AOB＝120°，连接OC，OP，

∵∠APB＝120°，

∴点P在以点O为圆心，OB为半径的圆上，

∵CP≥OCOP，

∴当点O，点P，点C共线时，PC有最小值，

∵OA＝OB，∠AOB＝120°，

∴∠ABO＝30°，

∴∠CBO＝90°，

∵OA＝OB，BC＝CA，OC＝OC，

∴△AOC△BOC（SSS），

∴∠ACO＝∠BCO＝30°，

∴CO＝2OB，

∵OC2OB2＝BC2，

∴3OB2＝16

∴OB＝，

∴OC＝

∴PC的最小值＝，

故答案为：．