Question

【题目】已知：矩形ABCD内接于⊙O，连接 BD，点E在⊙O上，连接 BE交 AD于点F，∠BDC+45°=∠BFD，连接ED．

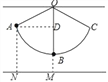
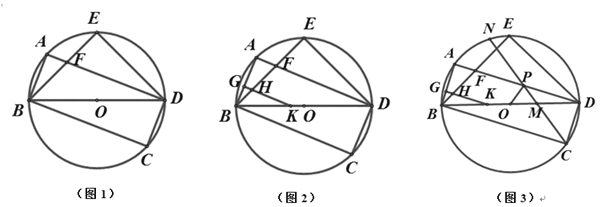
（1）如图 1，求证：∠EBD=∠EDB；

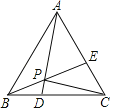
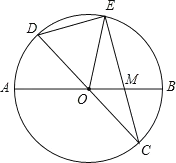
（2）如图2，点G是 AB上一点，过点G作 AB的垂线分别交BE和 BD于点H和点K，若HK=BG+AF，求证：AB=KG；

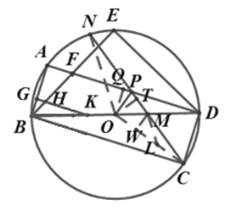
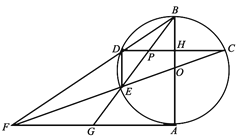
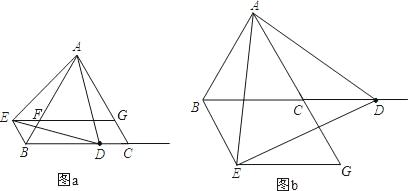
（3）如图 3，在（2）的条件下，⊙O上有一点N，连接 CN分别交BD和 AD于点 M和点 P，连接 OP，∠APO=∠CPO，若 MD=8，MC= 3，求线段 GB的长．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）GB．

【解析】

（1）根据矩形的性质可知∠BDC=∠DBA，∠A=90°，再结合已知条件∠BDC+45°=∠BFD，通过角的等量代换可得出∠EBD=45°，又因为∠BED=90°，即可得出结论；

（2）过点K 作 KS⊥BE，垂足为 R，交 AB 于点 S．证明△SRB≌△HRK，得出SB=HK，再证明△ABF≌△GKS，即可得出结论；

（3）过点 O 分别作AD 和 CN 的垂线，垂足分别为 Q 和 T，连接 OC．通过证明△OQD≌△OTC，得出AD=CN=BC，连接ON，证△NOC≌△BOC，得出∠BCO=∠NCO

设∠OBC=∠OCB=∠NCO=α，由此得出∠MOC=2α，过点 M 作 MW⊥OC，垂足为 W

在 OC 上取一点 L，使 WL=OW，连接 ML，设OM=ML=LC=a，根据勾股定理可求出OM的值,继而求出MW=3，WC=9，∴OB=OC=OD=13，BD=26，再解直角三角形即可．

解：（1）如图1，∵矩形 ABCD

∴AB∥CD，∠A=90°

∴∠BDC=∠DBA，BD是⊙O的直径

∴∠BED=90°

∵∠BFD=∠ABF+∠A，∠BFD=∠BDC+45°

∴∠ABF+∠A=∠BDC+45°

即∠ABF+90°=∠DBA+45°

∴∠DBA-∠ABF=45°

∴∠EBD=45°

∴∠EBD=∠EDB

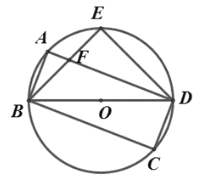
（2）证明：如下图 ，在图2中，过点K 作 KS⊥BE，垂足为 R，交 AB 于点 S．

∵KG⊥AB

∴∠BGH=∠KRH=∠SRB=∠KGS=90°

∴∠SBR=∠HKR

∵∠RBK=∠RKB=45°

∴BR=KR

∵∠SRB=∠HRK=90°

∴△SRB≌△HRK

∴SB=HK

∵SB=BG+SG，HK=BG+AF

∴BG+SG=BG+AF

∴SG=AF

∵∠ABF=∠GKS，∠BAF=∠KGS=90°

∴△ABF≌△GKS

∴AB=KG

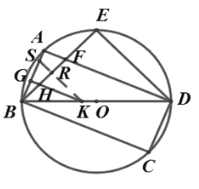
（3）如下图 ，在图3中，过点 O 分别作AD 和 CN 的垂线，垂足分别为 Q 和 T，连接 OC．

∵∠APO=∠CPO

∴OQ=OT

∵OD=OC，∠OQD=∠OTC=90°

∴△OQD≌△OTC

∴DQ=CT

∴AD=CN=BC

连接 ON

∵OC=OC，ON=OB

∴△NOC≌△BOC

∴∠BCO=∠NCO

设∠OBC=∠OCB=∠NCO=α

∴∠MOC=2α

过点 M 作 MW⊥OC，垂足为 W

在 OC 上取一点 L，使 WL=OW，连接 ML

∴MO=ML

∴∠MOL=∠MLO=2α

∴∠LCM=∠LMC=α

∴ML=CL

设OM=ML=LC=a

则OD=a+8=OC，∴OL=8，OW=WL=4

∵OM 2OW2MW2MC 2CW 2

∴

（9 舍去）， 5

∴OM=5

∴MW=3，WC=9，∴OB=OC=OD=13，BD=26

∵∠GKB=∠CBD=∠ADB=∠BCO=∠MCW，tan∠MCW=

∴tan∠GKB=tan∠CBD=tan∠ADB=tan∠BCO=tan∠MCW=

∴CD=GK=AB

在 Rt△GKB 中，tan∠GKB=

∴GB