题目内容
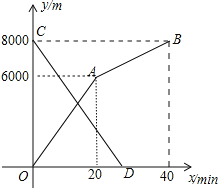
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 交于点
交于点![]() ,将点
,将点![]() 向右平移某个距离得到点
向右平移某个距离得到点![]() ,点
,点![]() 在抛物线上.已知点
在抛物线上.已知点![]() ,
,![]() .
.
(1) 当![]() 时.
时.
①求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
②求线段![]() 的长度;
的长度;
(2)若抛物线与线段![]() 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
【答案】(1)①![]() ,②
,②![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)①根据题意令![]() ,求出两个x的值,然后根据题意判断A的坐标即可;
,求出两个x的值,然后根据题意判断A的坐标即可;
②根据B,P两点的坐标即可求出BP的长度;
(2)先利用抛物线的性质判断出点Q在抛物线内,然后分两种情况:![]() 或
或![]() 时,分别讨论即可.
时,分别讨论即可.
解: (1) ①由己知得: ![]() ,
,
化简得:![]() ,
,
![]() ,
,
解得:![]() ,
,![]() .
.
∵![]() ,又点
,又点![]() 在点
在点![]() 的左侧,
的左侧,
∴![]() ;
;
②∵![]() ,
,![]() ,
,
∴![]() ;
;
(2)∵ ![]() ,令
,令![]() 时,
时,![]() ,
,
∴抛物线的对称轴为![]() ,与
,与![]() 轴交点坐标为
轴交点坐标为![]() ,
,
∴由抛物线的对称性可知![]() 必在抛物线上.
必在抛物线上.
又由己知![]() ,
,
∴![]() ,
,
即点![]() 必在抛物线内部.
必在抛物线内部.
当![]() 时,点
时,点![]() ,
,![]() ,
,
∴点![]() 一定在点
一定在点![]() 左侧即点
左侧即点![]() 一定在抛物线外部,
一定在抛物线外部,
∴当![]() 时,抛物线与线段
时,抛物线与线段![]() 恰有一个公共点.
恰有一个公共点.
当![]() 时,点
时,点![]() ,
,
若抛物线与线段![]() 恰有一个公共点,则
恰有一个公共点,则![]()
解得![]() .
.
综上所述:![]() 或
或![]() .
.

【题目】红旗连锁超市准备购进甲、乙两种绿色袋装食品.甲、乙两种绿色袋装食品的进价和售价如表.已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
甲 | 乙 | |
进价(元/袋) |
|
|
售价(元/袋) | 20 | 13 |
(1)求![]() 的值;
的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于4800元,且不超过4900元,问该超市有几种进货方案?
(3)在(2)的条件下,该超市如果对甲种袋裝食品每袋优惠![]() 元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
【题目】某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.假定每位顾客购买商品的可能性相同.
商品 顾客人数 | 甲 | 乙 | 丙 | 丁 |
100 | √ | × | √ | √ |
217 | × | √ | × | √ |
200 | √ | √ | √ | × |
300 | √ | × | √ | × |
85 | √ | × | × | × |
98 | × | √ | × | × |
(1)估计顾客同时购买乙和丙的概率为__________.
(2)如果顾客购买了甲,并且同时也在乙、丙、丁中进行了选购,则购买__________(填乙、丙、丁)商品的可能性最大.