题目内容
【题目】如图，ABCD中，AB∥x轴，AB＝6．点A的坐标为（1，﹣4），点D的坐标为（﹣3，4），点B在第四象限，点G是AD与y轴的交点，点P是CD边上不与点C，D重合的一个动点，过点P作y轴的平行线PM，过点G作x轴的平行线GM，它们相交于点M，将△PGM沿直线PG翻折，当点M的对应点落在坐标轴上时，点P的坐标为______．
【答案】（﹣
，4）或（，4）
【解析】
先求出点G坐标，由勾股定理可求M'N的长，再由勾股定理可求m的值，即可求解．
解：∵点A的坐标为（1，﹣4），点D的坐标为（﹣3，4），
∴直线AD解析式为：y＝﹣2x﹣2，
∴点G（0，﹣2），
如图1中，当点P在线段CD上时，设P（m，4）．
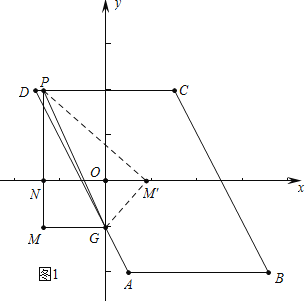
在Rt△PNM′中，∵PM＝PM′＝6，PN＝4，
∴NM′＝
＝2
，
在Rt△OGM′中，∵OG2+OM′2＝GM′2，
∴22+（2+m）2＝m2，
解得m＝﹣，
∴P（﹣，4）
根据对称性可知，P（，4）也满足条件．
故答案为：（﹣，4）或（，4）
练习册系列答案
同步练习河南大学出版社系列答案
相关题目
