题目内容
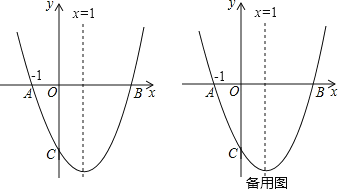
【题目】如图,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,且关于直线x=1对称,点A的坐标为(﹣1,0).
(1)求二次函数的表达式;
(2)连接BC,若点P在y轴上时,BP和BC的夹角为15°,求线段CP的长度;
(3)当a≤x≤a+1时,二次函数y=x2+bx+c的最小值为2a,求a的值.
【答案】(1)y=x2﹣2x﹣3;(2)CP的长为3﹣![]() 或3
或3![]() ﹣3;(3)a的值为1﹣
﹣3;(3)a的值为1﹣![]() 或2+
或2+![]() .
.
【解析】
(1)先根据题意得出点B的坐标,再利用待定系数法求解可得;
(2)分点P在点C上方和下方两种情况,先求出∠OBP的度数,再利用三角函数求出OP的长,从而得出答案;
(3)分对称轴x=1在a到a+1范围的右侧、中间和左侧三种情况,结合二次函数的性质求解可得.
(1)∵点A(﹣1,0)与点B关于直线x=1对称,
∴点B的坐标为(3,0),
代入y=x2+bx+c,得:
![]() ,
,
解得![]() ,
,
所以二次函数的表达式为y=x2﹣2x﹣3;
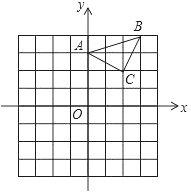
(2)如图所示:

由抛物线解析式知C(0,﹣3),
则OB=OC=3,
∴∠OBC=45°,
若点P在点C上方,则∠OBP=∠OBC﹣∠PBC=30°,
∴OP=OBtan∠OBP=3×![]() =
=![]() ,
,
∴CP=3﹣![]() ;
;
若点P在点C下方,则∠OBP′=∠OBC+∠P′BC=60°,
∴OP′=OBtan∠OBP′=3×![]() =3
=3![]() ,
,
∴CP=3![]() ﹣3;
﹣3;
综上,CP的长为3﹣![]() 或3
或3![]() ﹣3;
﹣3;
(3)若a+1<1,即a<0,
则函数的最小值为(a+1)2﹣2(a+1)﹣3=2a,
解得a=1﹣![]() (正值舍去);
(正值舍去);
若a<1<a+1,即0<a<1,
则函数的最小值为1﹣2﹣3=2a,
解得:a=﹣2(舍去);
若a>1,
则函数的最小值为a2﹣2a﹣3=2a,
解得a=2+![]() (负值舍去);
(负值舍去);
综上,a的值为1﹣![]() 或2+
或2+![]() .
.

 阅读快车系列答案
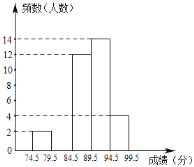
阅读快车系列答案【题目】为了庆祝中华人民共和国成立70周年,某市决定开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了下列不完整的统计图表.
分数段 | 频数 | 频率 |
74.5~79.5 | 2 | 0.05 |
79.5~84.5 | m | 0.2 |
84.5~89.5 | 12 | 0.3 |
89.5~94.5 | 14 | n |
94.5~99.5 | 4 | 0.1 |
(1)表中m=__________,n=____________;
(2)请在图中补全频数直方图;
(3)甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在_________分数段内;
(4)选拔赛中,成绩在94.5分以上的选手,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列举法或树状图法求恰好是一名男生和一名女生的概率.