Question

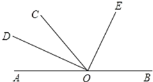
【题目】如图，O为直线AB上一点，∠AOC=50°，OD平分∠AOC，∠DOE=90°．

（1）求出∠BOD的度数；

（2）经测量发现：OE平分∠BOC，请通过计算说明道理．

Answer 1

【答案】（1）；（2）见解析.

【解析】

（1）利用角平分线性质求出∠AOD度数，然后利用补角性质进一步计算求解即可；

(2)根据角平分线性质求出∠DOC=25°，从而得出∠COE，进而根据∠BOC的度数进一步证明即可.

（1）∵∠AOC=50°，OD平分∠AOC，

∴∠AOD=25°，

∴∠BOD=180°∠AOD=155°；

（2）∵∠AOC=50°,

∴∠BOC=130°，

∵OD平分∠AOC，∠AOC=50°，

∴∠DOC=25°，

∵∠DOE=90°，

∴∠COE=90°25°=65°，

∴∠COE=∠BOC，

∴OE平分∠BOC.