题目内容
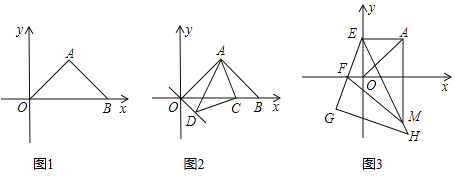
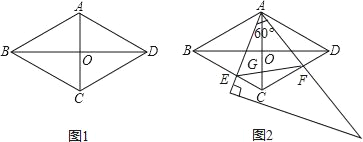
【题目】如图1,在菱形ABCD中,AC=2,BD=2![]() ,AC、BD相交于点O.
,AC、BD相交于点O.
(1)AB的长为 ;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.
①求证:△ABE≌△ACF;
②判断△AEF是哪一种特殊三角形,并说明理由.
【答案】(1)2;(2)①见解析;②△AEF是等边三角形,理由见解析
【解析】分析:(1)利用菱形对角线互相垂直且平分可得AO、OB,根据勾股定理求出即可;
(2)①由(1)知,菱形ABCD的边长是2,AC=2,然后由△ABC和△ACD是等边三角形,利用ASA可证得△ABE≌△ACF;
②由①可得AE=AF,根据有一个角是60°的等腰三角形是等边三角形推出即可.
详解:(1)∵在菱形ABCD中,AC=2,BD=2![]() ,
,
∴∠AOB=90°,OA=![]() AC=1,BO=
AC=1,BO=![]() BD=
BD=![]() ,
,
在Rt△AOB中,由勾股定理得:AB=![]() =2;
=2;
故答案为:2;
(2)①∵由(1)知,菱形ABCD的边长是2,AC=2,
∴△ABC和△ACD是等边三角形,
∴∠BAC=∠BAE+∠CAE=60°,
∵∠EAF=∠CAF+∠CAE=60°,
∴∠BAE=∠CAF,
在△ABE和△ACF中,
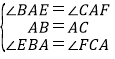 ,
,
∴△ABE≌△ACF(ASA),
②△AEF是等边三角形,
理由是:∵△ABE≌△ACF,
∴AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形.

练习册系列答案
相关题目