Question

【题目】阅读以下材料并回答问题：

材料一：已知点 Px0 , y0 和直线 y kx b ，则点Px0 , y0 到直线 y kx b 的距离 d 可以用公式表示为 d . 例如：求点 P 2,1到直线 y x 1的距离.

解：因为直线 y x 1可以变形为 x y 1 0 ，其中 k 1， b 1，则点 P 2,1到直线y x 1的距离可以表示为 d =.

材料二：对于直线 y1 k1 x b1 与直线 y2 k2 x b2 ，若 y1 // y2 ，那么 k1 k2 且b1 b2 ，若 y1 y2 ，那么 k1 k2 1.

（1）点 P1,1到直线 y 2x 1的距离为 ；

（2）已知直线 y1 x 与直线y2 k2 x 1平行，且在平面内存在点到直线 y2 k2 x 1的距离是其到直线 y1 x 距离的两倍，求点所在直线的解析式；

（3）已知直线与直线垂直，其交点为Q，在平面内存在点P(点P不在直线与直线上),过点P分别向直线与直作垂线，垂足分别为M、N，若MQNP是边长为的正方形，求点P点坐标.

Answer 1

【答案】（1）；（2）y=x-1或；（3）P（3，0）或（7，3）或（0，4）或（4，7）．

【解析】

（1）根据条件的P的坐标和点到直线的距离公式可以直接求出结论；

（2）根据平行得到k2的值，再根据点到直线的距离公式以及点到直线 y2 k2 x 1的距离是其到直线 y1 x 距离的两倍，列方程即可求出结论；

（3）设P（a，b）．由直线垂直，得出k0的值，再由P（a，b）到两条直线的距离都等于，列方程组就可以求出结论．

（1）∵点P（－1，1），∴点P到直线y=2x+1的距离为：

d．

（2）设满足条件的点的坐标为（x，y）．

∵直线 y1 x 与直线y2 k2 x 1平行，∴k2=1，∴y2 x 1．由题意，得：，∴，∴x-y+1=±2（x-y），即y=x-1或．

故点所在直线的解析式为y=x-1或．

（3）设P（a，b）．

∵直线与直线垂直，∴k0=，∴．

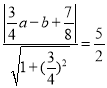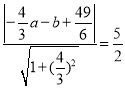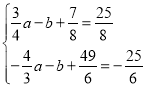∵MQNP是边长为的正方形，∴P（a，b）到两条直线的距离都等于，∴，，整理得：，，∴或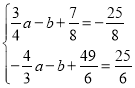或或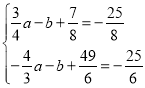，解方程组得：或或或，∴P（3，0）或（7，3）或（0，4）或（4，7）．