题目内容
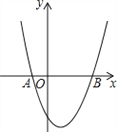
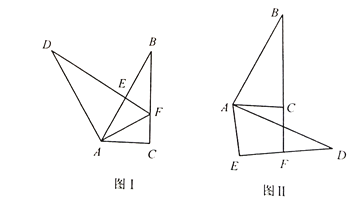
【题目】（1）如图1，在△ABC中，∠ACB=90°，点D在△ABC外，连接AD，作DE⊥AB，交BC于点F，AD=AB，AE=AC，连接AF，则DF，BC，CF间的等量关系是 ；
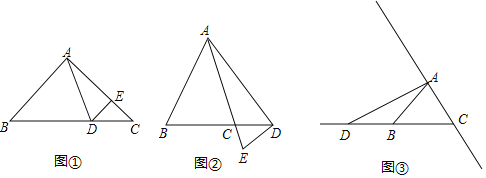
（2）如图2，AB=AD，AC=AE，∠ACB=∠AED=90°，延长BC交DE于点F，写出DF，BC，CF间的等量关系，并证明你的结论.
【答案】（1）
；（2）
；证明见解析处.
【解析】
（1）首先根据已知条件可判定
，得出
，再次利用同样的原理判定
，可得出
，进而得出三者的等量关系为；
（2）首先连接
，根据已知条件可判定
，得出
，再根据同理即可判定
，得出
，进而得出三者等量关系为.
解：（1）∵∠ACB=90°，DE⊥AB，
∴
又∵AD=AB，AE=AC，
∴
∴
又∵AE=AC，
，
∴
∴
又∵
∴
故答案为.
（2）
证明：连接，如图所示，
∵AB=AD，AC=AE，∠ACB=∠AED=90°，
∴
∴
又∵AC=AE，，
∴
∴
又∵
∴
练习册系列答案
小学课时特训系列答案
相关题目
【题目】随机抽取某城市天的空气质量状况统计如下：
污染指数（ |
|
|
|
|
|
|
天数（ |
|
|
|
|
|
|
（其中
时，空气质量为优；
时，空气质量为良；
时，空气质量为轻微污染）
（1）这
天中，空气质量为轻微污染的天数所占的百分数是多少？
（2）估计该城市一年（以
天记）中有多少天空气质量到良以上？
（3）保护环境人人有责，请说出一种保护环境的好方法.
