题目内容
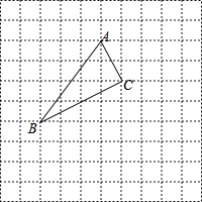
【题目】 如图，把△ABC放置在每个小正方形边长为1的网格中，点A，B，C均在格点上，建立适当的平面直角坐标系xOy，使点A（1，4），△ABC与△A'B'C'关于y轴对称．
（1）画出该平面直角坐标系与△A'B'C'；
（2）在y轴上找点P，使PC+PB'的值最小，求点P的坐标与PC+PB'的最小值．
【答案】（1）详见解析；（2）图详见解析，点P的坐标为（0，1），PC+PB'的最小值为2
．
【解析】
（1）根据点A的坐标找到坐标原点并建立坐标系，然后分别找到A、B、C关于y轴的对称点A'、B'、C' ，连接A'B'、B'C' 、A'C'即可；
（2）直接利用轴对称求最短路线的方法、利用待定系数法求一次函数的解析式以及勾股定理得出答案．
解：（1）根据点A的坐标找到坐标原点并建立坐标系，然后分别找到A、B、C关于y轴的对称点A'、B'、C' ，连接A'B'、B'C' 、A'C'，如图所示：△A'B'C'即为所求；
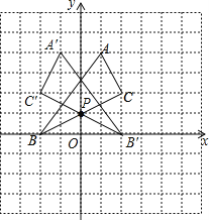
（2）如图所示：BC与y轴交于点P，根据对称的性质可得PB= PB'
∴PC+PB'=PC＋PB=BC，根据两点之间线段最短，此时PC+PB'最小，且最小值即为BC的长
设直线BC的解析式为y=kx＋b
将B、C坐标代入，得
解得：
∴直线BC的解析式为
当x=0时，y=1
∴点P的坐标为：（0，1），
PC+PB'的最小值为：
=2．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
