Question

【题目】如图，AB是O的直径，AE交O于点E，且与O的切线CD互相垂直，垂足为D．
（1）求证：∠EAC=∠CAB；
（2）若CD=4，AD=8：①求O的半径；②求tan∠BAE的值．

Answer 1

【答案】
（1）证明：连接OC．

∵CD是⊙O的切线，

∴CD⊥OC，

又∵CD⊥AE，

∴OC∥AE，

∴∠1=∠3，

∵OC=OA，

∴∠2=∠3，

∴∠1=∠2，

即∠EAC=∠CAB；

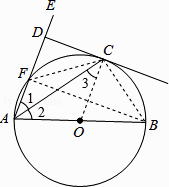
（2）解：①连接BC．

∵AB是⊙O的直径，CD⊥AE于点D，

∴∠ACB=∠ADC=90°，

∵∠1=∠2，

∴△ACD∽△ABC，

∴ ，

∵AC2=AD2+CD2=42+82=80，

∴AB= =10，

∴⊙O的半径为10÷2=5．

②连接CF与BF．

∵四边形ABCF是⊙O的内接四边形，

∴∠ABC+∠AFC=180°，

∵∠DFC+∠AFC=180°，

∴∠DFC=∠ABC，

∵∠2+∠ABC=90°，∠DFC+∠DCF=90°，

∴∠2=∠DCF，

∵∠1=∠2，

∴∠1=∠DCF，

∵∠CDF=∠CDF，

∴△DCF∽△DAC，

∴ ，

∴DF= =2，

∴AF=AD﹣DF=8﹣2=6，

∵AB是⊙O的直径，

∴∠BFA=90°，

∴BF= =8，

∴tan∠BAD= ．

【解析】（1）首先连接OC，由CD是⊙O的切线，CD⊥OC，又由CD⊥AE，即可判定OC∥AE，根据平行线的性质与等腰三角形的性质，即可证得∠EAC=∠CAB；（2）①连接BC，易证得△ACD∽△ABC，根据相似三角形的对应边成比例，即可求得AB的长，继而可得⊙O的半径长；②连接CF与BF．由四边形ABCF是⊙O的内接四边形，易证得△DCF∽△DAC，然后根据相似三角形的对应边成比例，求得AF的长，又由AB是⊙O的直径，即可得∠BFA是直角，利用勾股定理求得BF的长，即可求得tan∠BAE的值．