题目内容
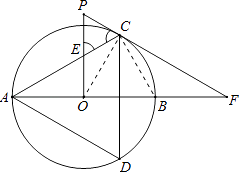
【题目】如图,以AB为直径的⊙O是△ADC的外接圆,过点O作PO⊥AB,交AC于点E,PC的延长线交AB的延长线于点F,∠PEC=∠PCE. 
(1)求证:FC为⊙O的切线;
(2)若△ADC是边长为a的等边三角形,求AB的长.(用含a的代数式表示)
【答案】
(1)证明:连接OC.
∵OA=OC(⊙O的半径),
∴∠EAO=∠ECO(等边对等角).
∵PO⊥AB,∴∠EAO+∠AEO=90°(直角三角形中的两个锐角互余).
∵∠PEC=∠PCE(已知),∠PEC=∠AEO(对顶角相等)
∴∠AEO=∠PCE(等量代换),
∴∠PCO=∠ECO+∠PCE=∠EAO+∠AEO=90°.即OC⊥FC,
∵点C在⊙O上,
∴FC为⊙O的切线
(2)解:连接BC.

∵AB是⊙O的直径,∴∠ACB=90°.
∵△ADC是边长为a的等边三角形,
∴∠ABC=∠D=60°,AC=a.
在Rt△ACB中,∵sin∠ABC= ![]()
∴AB= ![]() =
= ![]() a.
a.
【解析】(1)连接OC.欲证FC为⊙O的切线,只需证明OC⊥FC即可;(2)连接BC.由等边三角形的性质、“同弧所对的圆周角相等”推知∠ABC=∠ADC=60°;然后在直角△ABC中利用正弦三角函数的定义来求AB线段的长度.
【考点精析】掌握等边三角形的性质和切线的判定定理是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目






