题目内容
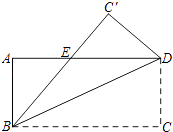
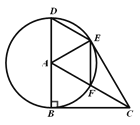
【题目】在Rt△ABC中,∠ABC=90°,以点A为圆心,AB为半径,作⊙A交AC于点F,交BA的延长线于点D,过点D作AC的平行线交⊙A于点E,连接AE、CE,EF.
⑴求证:CE⊥AE;
⑵当∠CAB等于多少度时,四边形ADEF为菱形,并给于证明.
【答案】(1)证明见解析;
(2)当∠CAB =60°多少度时,四边形ADFE为菱形,证明见解析.
【解析】在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作OA交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交OA于点F,连接AF、BF,DF.
解:(1)证明:∵EF∥AB,
∴∠E=∠CAB,∠EFA=∠FAB.∵∠E=∠EFA .∠FAB=∠CAB.
在△ABC和△ABF中,
AF=AC,∠FAB=∠CAB,AB=AB,
∵△ABG≌△ABF,∴∠AFB=∠ACB=90°,
∴BF⊥AF.
(2)当∠CAB=60°时,四边形ADFE为菱形,
证明:∵∠ CAB=60°.
∴∠FAB=∠CAB=∠ CAB=60°.
∴EF=AD=AE.
∴四边形ADFE是菱形,
“点睛”本题考查了菱形的判定、全等三角形的判定与性质及圆周角定理的知识,解题的关键是了解菱形的判定方法及全等三角形的判定方法,难度不大.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目