题目内容
【题目】解不等式(组)
(1)2x﹣7≤3(x﹣1)
(2) 并写出它的整数解.
并写出它的整数解.
【答案】
(1)解:2x﹣7≤3(x﹣1),
2x﹣7≤3x﹣3,
2x﹣3x≤﹣3+7,
﹣x≤4,
x≥﹣4
(2)解: 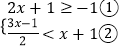
∵解不等式①得:x≥﹣1,
解不等式②得:x<3,
∴不等式组的解集为﹣1≤x<3,
∴不等式组的整数解为﹣1,0,1,2
【解析】(1)去括号,移项,合并同类项,系数化成1即可;(2)求出每个不等式的解集,再求出不等式组的解集,即可得出答案.
【考点精析】通过灵活运用一元一次不等式的解法和一元一次不等式组的解法,掌握步骤:①去分母;②去括号;③移项;④合并同类项; ⑤系数化为1(特别要注意不等号方向改变的问题);解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )即可以解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目