Question

【题目】如图，将长方形ABCD沿着对角线BD折叠，使点C落在C′处，BC′交AD于点E．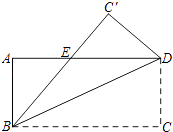
（1）试判断△BDE的形状，并说明理由；
（2）若AB=4，AD=8，求△BDE的面积．

Answer 1

【答案】
（1）解：△BDE是等腰三角形．

由折叠可知，∠CBD=∠EBD，

∵AD∥BC，

∴∠CBD=∠EDB，

∴∠EBD=∠EDB，

∴BE=DE，

即△BDE是等腰三角形

（2）解：设DE=x，则BE=x，AE=8﹣x，

在Rt△ABE中，由勾股定理得：AB2+AE2=BE2即42+（8﹣x）2=x2，

解得：x=5，

所以S△BDE= DE×AB= ×5×4=10

【解析】（1）由折叠可知，∠CBD=∠EBD，再由AD∥BC，得到∠CBD=∠EDB，即可得到∠EBD=∠EDB，于是得到BE=DE，等腰三角形即可证明；（2）设DE=x，则BE=x，AE=8﹣x，在Rt△ABE中，由勾股定理求出x的值，再由三角形的面积公式求出面积的值．