��Ŀ����
����Ŀ��3�·ݣ�ijƷ�Ƴ�����ʽ�������ۣ�3 ��1�յ�������Ϊ10����3��2�յ�������Ϊ35�����Ժ�ÿ�����������ǰһ���25����ֱ�����������ﵽ������������ʼ�����½������ˣ�ÿ�����������ǰһ����15����ֱ��3��31��������Ϊ0�����Ʒ�Ƴ��µ�������Ϊp����������������Ϊn���գ���p��n֮��Ĺ�ϵ��ͼ��ʾ��
��1����3�� ��ʱ,�����������.
��2��д��p����n�ĺ�����ϵʽ��ע��n ��ȡֵ��Χ����
��3�����о���������Ʒ�Ƴ��µ�����������150����ʱ��Ϊ��Ʒ�Ƴ��µ������ڣ����ʣ���Ʒ�Ƴ��±�����������������Ƕ����죿
���𰸡���1��12
��2��p����n�ĺ�����ϵʽ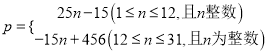
��3����Ʒ�Ƴ��±������������������14��.
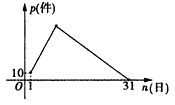
����������1����Ϊ5��1����������Ϊ10����5��2����������Ϊ35�����Ժ�ÿ�����������ǰһ���25����ֱ�����������ﵽ������������ʼ�����½������ˣ�ÿ�����������ǰһ����15����ֱ��5��31��������Ϊ0������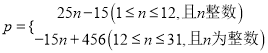
��2����1��n��12ʱ��12��n��31��������г�����ʽ���ֱ����n��ȡֵ��Χ���ɣ�
��3����12��Ϊ�磬ǰ���������Ȳ����� �� 1��n��12ʱ������a1=10��ĩ��a12=285������ k1=12 ���� �� s1=��10+285����![]() =1770 �� 12��n��31ʱ������a13=270��ĩ��a31=0������ k2=19 ���� �� s1=270��
=1770 �� 12��n��31ʱ������a13=270��ĩ��a31=0������ k2=19 ���� �� s1=270��![]() =2565���������ͼ��ɣ�
=2565���������ͼ��ɣ�
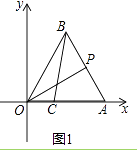
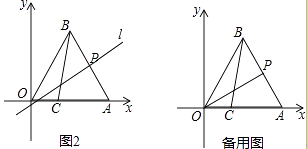
�⣺(1)��3��x�����һ�����������ӵ����ڣ�������ã�
![]() �����
�����![]()
��2���ɣ�1����![]() ��
��![]()
��3����![]() ��
��![]() �����
�����![]() ������ʵ�����ڣ�
������ʵ�����ڣ�
Ӧ��7�����㣬�˶�ʱ��������Ϊ12-7+1=6��
��![]() ���ʴ˶�������Ϊ
���ʴ˶�������Ϊ
20-12=8�졣���6+8=14��
���㾦�����⿼����һ�κ��������ã�һ�κ�����ͼ�����������ã����һ�κ����Ľ���ʽ�����ã����ʱ�������������ϸ�۲�ͼ�����÷ֶκ�����������ǽ���ؼ���