题目内容
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( ) 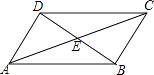
A.6
B.12
C.20
D.24
【答案】D
【解析】解:在Rt△BCE中,由勾股定理,得 CE= ![]() =
= ![]() =5.
=5.
∵BE=DE=3,AE=CE=5,
∴四边形ABCD是平行四边形.
四边形ABCD的面积为BCBD=4×(3+3)=24,
故选:D.
【考点精析】关于本题考查的勾股定理的概念和平行四边形的判定与性质,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能得出正确答案.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目