题目内容
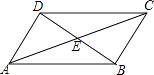
【题目】如图,在ABCD中,BD=2AB,AC与BD相交于点O,点E、F、G分别是OC、OB、AD的中点. 求证: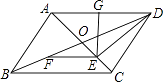
(1)DE⊥OC;
(2)EG=EF.
【答案】
(1)证明:∵四边形ABCD是平行四边形,AC与BD相交于点O,
∴BD=2OD,AB=CD,AD=BC.
∵BD=2AB,
∴OD=AB=CD.
∵点E是OC的中点,
∴DE⊥OC
(2)证明:∵DE⊥OC,点G是AD的中点,
∴EG= ![]() AD;
AD;
∵点E、F分别是OC、OB的中点.
∴EF= ![]() BC.
BC.
∵AD=BC,
∴EG=EF
【解析】(1)由四边形ABCD是平行四边形,AC与BD相交于点O,根据平行四边形的性质,即可得BD=2OD,AB=CD,AD=BC,又由BD=2AB,可得△ODC是等腰三角形,根据三线合一的性质,即可证得DE⊥OC;(2)由DE⊥OC,点G是AD的中点,利用直角三角形斜边上的中线等于斜边的一半,即可得EG= ![]() AD,又由三角形中位线的性质,求得EF=
AD,又由三角形中位线的性质,求得EF= ![]() BC,则可证得EG=EF.
BC,则可证得EG=EF.
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识,掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半,以及对平行四边形的性质的理解,了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

【题目】为了了解业余射击队队员的射击成绩,对某次射击比赛中每一名队员的平均成绩(单位:环,环数为整数)进行了统计,分别绘制了如下统计表和频率分布直方图,请你根据统计表和频率分布直方图回答下列问题: 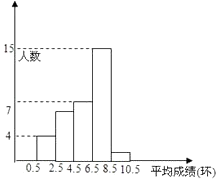
平均成绩 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
人数 | 0 | 1 | 3 | 3 | 4 | 6 | 1 | 0 |
(1)参加这次射击比赛的队员有多少名?
(2)这次射击比赛平均成绩的中位数落在频率分布直方图的哪个小组内?
(3)这次射击比赛平均成绩的众数落在频率分布直方图的哪个小组内?