��Ŀ����
����Ŀ��������̽����
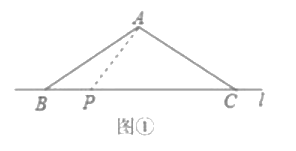
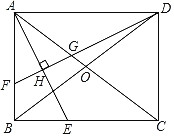
��ͼ���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AEƽ�֡�BAC����BC�ڵ�E����DF��AE�ڵ�H���ֱ�AB��AC�ڵ�F��G��
��1���жϡ�AFG����״��˵�����ɣ�
��2����֤��BF=2OG��
��Ǩ��Ӧ�ã�
��3���ǡ�DGO�����ΪS1����DBF�����ΪS2����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
����չ���죩
��4����DF������AB�ڵ�F��������̽�����е������������䣬����EF������BEF�����Ϊ����ABCD�����![]() ʱ����ֱ��д��tan��BAE��ֵ��
ʱ����ֱ��д��tan��BAE��ֵ��
���𰸡���1�����������Σ����ɼ���������2������������3��![]() ����4��
����4��![]() ��
��![]()
��������
��1����ͼ1�У���AFG�ǵ��������Σ�����ȫ�������ε�����֤�����ɣ�
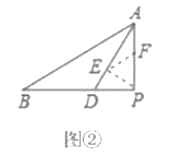
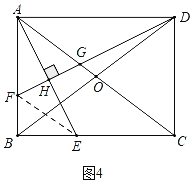
��2����ͼ2�У�����O��OL��AB��DF��L�����AFG=��OLG������֤��OG=OL����֤��BF=2OL���ɽ�����⣮
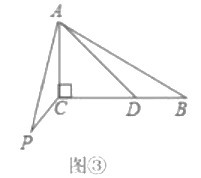
��3����ͼ3�У�����D��DK��AC��K�����DKA=��CDA=90�����������������ε����ʽ�����⼴�ɣ�
��4����OG=a��AG=k�����������Σ�����ͼ4�У�����EF������F���߶�AB��ʱ����G��OA�ϣ�����ͼ5�У�����F��AB���ӳ�����ʱ����G���߶�OC�ϣ�����EF���ֱ���⼴�ɽ�����⣮
��1���⣺��ͼ1�У���AFG�ǵ��������Σ�

���ɣ���AEƽ�֡�BAC��
���1=��2��
��DF��AE��
���AHF=��AHG=90����
��AH=AH��
���AHF�ա�AHG��ASA����
��AF=AG��
���AFG�ǵ��������Σ�
��2��֤������ͼ2�У�����O��OL��AB��DF��L�����AFG=��OLG��
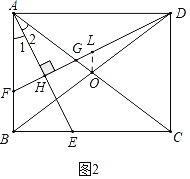
��AF=AG��
���AFG=��AGF��
�ߡ�AGF=��OGL��
���OGL=��OLG��
��OG=OL��
��OL��AB��
���DLO�ס�DFB��
��![]() ��
��
���ı���ABCD�Ǿ��Σ�
��BD=2OD��
��BF=2OL��
��BF=2OG��
��3���⣺��ͼ3�У�����D��DK��AC��K�����DKA=��CDA=90����
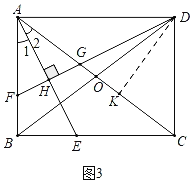
�ߡ�DAK=��CAD��
���ADK�ס�ACD��
��![]() ��
��
��S1=![]() OGDK��S2=
OGDK��S2=![]() BFAD��
BFAD��
�֡�BF=2OG��![]() ��
��
��![]() ����CD=2x��AC=3x����AD=
����CD=2x��AC=3x����AD= ![]() ��
��
��![]() ��
��
��4���⣺��OG=a��AG=k��
����ͼ4�У�����EF������F���߶�AB��ʱ����G��OA�ϣ�
��AF=AG��BF=2OG��
��AF=AG=k��BF=2a��
��AB=k+2a��AC=2��k+a����
��AD2=AC2��CD2=[2��k+a��]2����k+2a��2=3k2+4ka��
�ߡ�ABE=��DAF=90������BAE=��ADF��
���ABE�ס�DAF��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�����⣺![]() =AD��k+2a����
=AD��k+2a����
��AD2=10ka��
��10ka=3k2+4ka��
��k=2a��
��AD= ![]() ��
��
��BE= ![]() =
= ![]() ��AB=4a��
��AB=4a��
��tan��BAE= ![]() ��
��
����ͼ5�У�����F��AB���ӳ�����ʱ����G���߶�OC�ϣ�����EF��
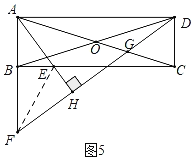
��AF=AG��BF=2OG��
��AF=AG=k��BF=2a��
��AB=k��2a��AC=2��k��a����
��AD2=AC2��CD2=[2��k��a��]2����k��2a��2=3k2��4ka��
�ߡ�ABE=��DAF=90������BAE=��ADF��
���ABE�ס�DAF��
��![]() ��
��
��![]() ��
��
�� ![]() ��
��
�����⣺![]() =AD/span>��k��2a����
=AD/span>��k��2a����
��AD2=10ka��
��10ka=3k2��4ka��
��k= ![]() ��
��
��AD= ![]() ��
��
��![]() ��AB=
��AB= ![]() ��
��
��tan��BAE= ![]() ��
��
����������tan��BAE��ֵΪ![]() ��
��![]() ��
��

 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�