题目内容
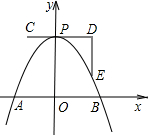
如图,从O点射出炮弹落地点为D,弹道轨迹是抛物线,若击中目标C点,在A测C的仰角∠BAC=45°,在B测C的仰角∠ABC=30°,AB相距(1+
)km,OA=2km,AD=2km.
(1)求抛物线解析式;
(2)求抛物线对称轴和炮弹运行时最高点距地面的高度.
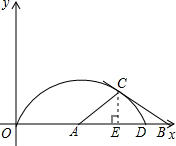
| 3 |
(1)求抛物线解析式;
(2)求抛物线对称轴和炮弹运行时最高点距地面的高度.

(1)过C作CE⊥OB交OB于E,设CE=xkm,
∵∠BAC=45°,
∴AE=CE=xkm,
∵AB相距(1+
)km,
∴BE=(1+
-x)km,
∵∠ABC=30°,
∴tan30°=
=
=
,
解得:x=1,
∴CE=AE=1km,
∵OA=2km,AD=2km,
∴OD=4km,OE=3km,
∴C的坐标为(3,1),D的坐标为(4,0)
设此抛物线解析式为y=ax2+bx+c,则
,
解得:
,
∴y=-
x2+
x;
(2)∵y=-
x2+
x=-
(x-2)2+
,
∴抛物线对称轴为x=2,炮弹运行时最高点距地面的高为
km.

∵∠BAC=45°,
∴AE=CE=xkm,
∵AB相距(1+
| 3 |
∴BE=(1+
| 3 |
∵∠ABC=30°,
∴tan30°=
| CE |
| BE |
| x | ||
1+
|
| ||
| 3 |
解得:x=1,
∴CE=AE=1km,
∵OA=2km,AD=2km,
∴OD=4km,OE=3km,
∴C的坐标为(3,1),D的坐标为(4,0)
设此抛物线解析式为y=ax2+bx+c,则
|
解得:
|
∴y=-
| 1 |
| 3 |
| 4 |
| 3 |
(2)∵y=-
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
∴抛物线对称轴为x=2,炮弹运行时最高点距地面的高为
| 4 |
| 3 |


练习册系列答案
相关题目

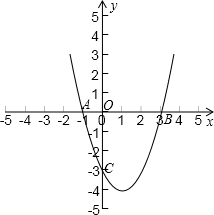 于A、B两点(如图),点C的坐标为(0,-3),且BO=CO
于A、B两点(如图),点C的坐标为(0,-3),且BO=CO