Question

【题目】已知等腰△ABC中，∠BAC=90°，BC=4，P为BC上一动点，∠MPN=45°，PM、PN分别与AB、AC交于点E、F，且PM⊥AB，BE=x.

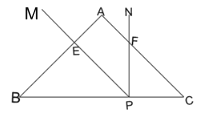
(1)若P点在BC上运动，求四边形AEPF的面积（用x的代数式表示）并写出x的取值范围

(2)当点P在BC上运动时，△EPF能否为直角三角形，若能，请写出此时x的值；若不能，请说明理由.

Answer 1

【答案】（1）四边形AEPF的面积＝；（2）x的值为或.

【解析】

（1）首先证明△ABC、△BEP、△FPC是等腰直角三角形，然后根据等腰直角三角形的边之间的关系求出AB、BP和PC，根据四边形AEPF的面积＝列式整理，然后求出AF，根据AF大于0以及AB=可得x的取值范围；

（2）由∠MPN=45°可知当△EPF为直角三角形时，△EPF是等腰直角三角形，然后分情况讨论：①当∠EFP＝90°时，②当∠FEP＝90°时，分别根据等腰直角三角形的边之间的关系列出方程求解即可.

解：（1）∵△ABC是等腰直角三角形，且PM⊥AB，

∴△BEP是等腰直角三角形，

∵∠MPN=45°，

∴∠BPN＝90°，即PN⊥BC，

∴△FPC是等腰直角三角形，

∵BC=4，BE=x，

∴AB=AC=，BP=，

∴PC=PF=，

∴四边形AEPF的面积＝，

，

，

，

∵PC=PF=，

∴CF=，

∴AF=AC-CF=，

∵AF＞0，即，

∴，

又∵AB=，

∴，

故四边形AEPF的面积＝；

（2）∵∠MPN=45°，

∴当△EPF为直角三角形时，△EPF是等腰直角三角形，

分情况讨论：

①当∠EFP＝90°时，EP为斜边，

由（1）可知，EP=x，PF=，

∴EP=PF，即，

解得：；

②当∠FEP＝90°时，FP为斜边，

由（1）可知，EP=x，PF=，

∴PF=EP，即，

解得：，

综上所述，当△EPF为直角三角形时，x的值为或.