题目内容
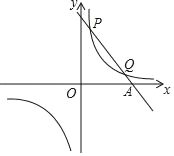
【题目】已知一次函数y＝k1x+b与反比例函数y＝
的图象交于第一象限内的P（
，8），Q（4，m）两点，与x轴交于A点．
（1）写出点P关于原点的对称点P′的坐标；
（2）分别求出这两个函数的表达式；
（3）求∠P′AO的正切值．
【答案】（1）（﹣
，﹣8）；（2）y＝﹣2x+9；（3）
．
【解析】
（1）根据中心对称的性质，可得点P关于原点的对称点P'的坐标；
（2）根据P（，8），可得反比例函数解析式，根据P（，8），Q（4，1）两点可得一次函数解析式；
（3）过点P′作P′B⊥x轴，垂足为B，构造直角三角形，依据P'B以及AB的长，即可得到∠P'AO的正切值．
解：（1）点P关于原点的对称点P′的坐标是（﹣，﹣8）；
（2）∵P（，8）在y＝
的图象上
∴k2＝×8＝4
∴反比例函数的表达式是：y＝
∵Q（4，m）在y＝的图象上
∴4×m＝4，即m＝1
∴Q（4，1）
∵y＝k1x+b过P（，8）、Q（4，1）两点
∴
解得：
∴一次函数的解析式是y＝﹣2x+9；
（3）作P'B⊥x轴于B，则P'B＝8，BO＝
对于y＝﹣2x+9，令y＝0，则x＝
∴AB＝+＝5
在Rt△ABP'中
tan∠P′AO＝
,
单元期中期末卷系列答案
【题目】行驶中的汽车，在刹车后由于惯性的原因，还要继续向前滑行一段距离才能停住，这段距离称为“刹车距离”．为了测定某种型号汽车的刹车性能，对这种汽车的刹车距离进行测试，测得的数据如下表：
刹车时车速(千米/时) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
刹车距离(米) | 0 | 0.1 | 0.3 | 0.6 | 1 | 1.6 | 2.1 |
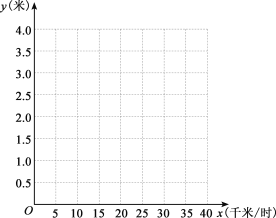
（1）在如图所示的直角坐标系中，以刹车时车速为横坐标，以刹车距离为纵坐标，描出这些数据所表示的点，并用平滑的曲线连结这些点，得到某函数的大致图象；
（2）测量必然存在误差，通过观察图象估计函数的类型，求出一个大致满足这些数据的函数表达式；
（3）一辆该型号汽车在高速公路上发生交通事故，现场测得刹车距离约为40米，已知这条高速公路限速100千米/时，请根据你确定的函数表达式，通过计算判断在事故发生时，汽车是否超速行驶．
