题目内容
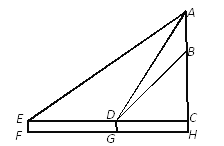
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,经过点A作AE⊥OC,垂足为点D,AE与BC交于点F,与过点B的直线交于点E,且EB=EF.
(1)求证:BE是⊙O的切线;
(2)若CD=1,cos∠AEB=![]() ,求BE的长.
,求BE的长.

【答案】(1)见解析;(2)BE=![]()
【解析】
(1)由OB=OC可得∠OBC=∠OCB,由EB=EF可知∠EBC=∠EFB,根据∠AFC+∠OCB=90°可知∠EBC+∠OBC=90°,即可得结论;
(2)由(1)可知∠AEB+∠EAB=90°,由∠AOD+∠EAB=90°即可证明∠AOD=∠AEB,设⊙O的半径为r,根据cos∠AOD=cos∠AEB=![]() 可求出r的值,即可得AB的值,根据cos∠AEB=
可求出r的值,即可得AB的值,根据cos∠AEB=![]() =
=![]() 可得AE=
可得AE=![]() BE,利用勾股定理求出BE的长即可.
BE,利用勾股定理求出BE的长即可.
(1)∵B、C在⊙O上,
∴OB=OC,
∴∠OBC=∠OCB,
∵EF=EB,
∴∠EBC=∠EFB,
又∵∠AFC=∠EFB,
∴∠AFC=∠EBC,
∵AE⊥OC,
∴∠AFC+∠OCB=90°,
∴∠EBC+∠OBC=90°,即BE⊥OB,
又OB是⊙O的半径,
∴EB是⊙O的切线;
(2)设⊙O的半径为r,则OA=OC=r,
又CD=1,
∴OD=r﹣1,
∵∠AOD+∠EAB=90°,∠AEB+∠EAB=90°,
∴∠AOD=∠AEB,
∴cos∠AOD=cos∠AEB=![]() ,
,
∴在Rt△AOD中,cos∠AOD=![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:r=![]() ,
,
∵AB是⊙O的直径,
∴AB=5,
在Rt△AEB中,cos∠AEB=![]() =
=![]() ,
,
∴AE=![]() BE,
BE,
又AE2=AB2+BE2,即(![]() BE)2=BE2+52,
BE)2=BE2+52,
解得:BE=![]() .
.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目