题目内容
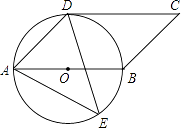
【题目】已知,如图,AB是⊙O的直径,C为⊙O上一点,AD垂直于经过点C的直线DE,垂足为点D,AC平分∠DAB.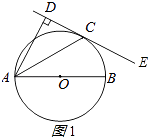
(1)求证:直线DE是⊙O的切线;
(2)连接BC,猜想:∠ECB与∠CAB的数量关系,并证明你的猜想.
【答案】
(1)
证明:连接OC,如图1所示:
∵OA=OC,
∴∠BAC=∠ACO,
∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠ACO=∠DAC,
∴AD∥OC,
∵AD⊥DE,
∴OC⊥DE,
∴直线DE是⊙O的切线;
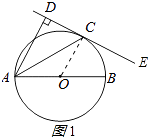
(2)
解:如图2所示:∠ECB=∠CAB,理由如下:
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAB+∠B=90°,
∵OC⊥DE,
∴∠ECB+∠BCO=90°,
∵OC=OB,
∴∠B=∠BCO,
∴∠ECB=∠CAB.
【解析】(1)连接OC,由等腰三角形的性质和已知条件得出∠ACO=∠DAC,证出AD∥OC,再由已知条件得出OC⊥DE,即可得出直线DE是⊙O的切线;(2)由圆周角定理得出∠ACB=90°,得出∠CAB+∠B=90°,得出∠ECB+∠BCO=90°,由等腰三角形的性质得出∠B=∠BCO,即可得出结论.
【考点精析】根据题目的已知条件,利用切线的性质定理的相关知识可以得到问题的答案,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校八年级一班20名女生某次体育测试的成绩统计如下:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)如果这20名女生体育成绩的平均分数是82分,求x、y的值;
(2)在(1)的条件下,设20名学生测试成绩的众数是a,中位数是b,求![]() 的值.
的值.