题目内容
【题目】问题探究:
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.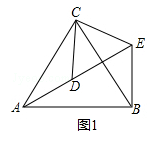
(1)证明:AD=BE;
(2)求∠AEB的度数.
(3)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.(Ⅰ)请求出∠AEB的度数;(Ⅱ)判断线段CM、AE、BE之间的数量关系,并说明理由.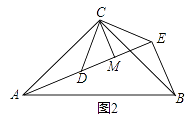
【答案】
(1)
证明:∵△ACB和△DCE均为等边三角形,
∴∠ACB=∠DCE=60°,CA=CB,CD=CE,
∴∠ACD=∠BCE,
在△CDA和△CEB中,
 ,
,
∴△CDA≌△CEB,
∴AD=BE
(2)
解:∵△CDA≌△CEB,
∴∠CEB=∠CDA=120°,
又∠CED=60°,
∴∠AEB=120°﹣60°=60°
(3)
解:(Ⅰ)∵△ACB和△DCE均为等腰直角三角形,
∠ACB=∠DCE=90°,
∴AC=BC,CD=CE,
∠ACB=∠DCB=∠DCE﹣∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,
 ,
,
∴△ACD≌△BCE,
∴AD=BE,∠BEC=∠ADC=135°.
∴∠AEB=∠BEC﹣∠CED=135°﹣45°=90°;
(Ⅱ)AE=2CM+BE,
在等腰直角三角形DCE中,CM为斜边DE上的高,
∴CM=DM=ME,
∴DE=2CM.
∴AE=DE+AD=2CM+BE
∴AE=2CM+BE
【解析】问题探究:(1)证明△CDA≌△CEB,根据全等三角形的性质解答;(2)根据全等三角形的性质得到∠CEB=∠CDA=120°,计算即可;
问题变式:(Ⅰ)证明△CDA≌△CEB,根据全等三角形的性质解答;(Ⅱ)根据全等三角形的性质、直角三角形的性质解答.

【题目】LED灯具有环保节能、投射范围大、无频闪、使用寿命较长等特点,在日常生活中,人们更倾向于LED灯的使用,某校数学兴趣小组为了解LED灯泡与普通白炽灯泡的销售情况,进行了市场调查:某商场购进一批30瓦的LED灯泡和普通白炽灯泡进行销售,其进价与标价如下表:
LED灯泡 | 普通白炽灯泡 | |
进价(元) | 45 | 25 |
标价(元) | 60 | 30 |

(1)该商场购进了LED灯泡与普通白炽灯泡共300个,LED灯泡按标价进行销售,而普通白炽灯泡打九折销售,当销售完这批灯泡后可以获利3200元,求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进两种灯泡120个,在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的30%,并求出此时这批灯泡的总利润为多少元?