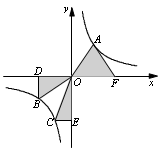
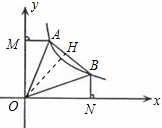
题目内容
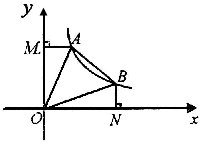
如图,直线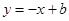 (b>0)与双曲线
(b>0)与双曲线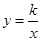 (
( >0)交于A、B两点,连接OA、OB, AM⊥
>0)交于A、B两点,连接OA、OB, AM⊥ 轴于M,BN⊥X轴于N;有以下结论:①OA =OB;②△AOM≌△BON;③若∠AOB=45°,则S△AOB=k;④AB=
轴于M,BN⊥X轴于N;有以下结论:①OA =OB;②△AOM≌△BON;③若∠AOB=45°,则S△AOB=k;④AB=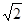 时,ON=BN=1,其中结论正确的是( )
时,ON=BN=1,其中结论正确的是( )
A. ①②③④ B. ①②③ C. ①② D. ①②④
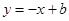 (b>0)与双曲线
(b>0)与双曲线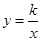 (
( >0)交于A、B两点,连接OA、OB, AM⊥
>0)交于A、B两点,连接OA、OB, AM⊥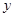 轴于M,BN⊥X轴于N;有以下结论:①OA =OB;②△AOM≌△BON;③若∠AOB=45°,则S△AOB=k;④AB=
轴于M,BN⊥X轴于N;有以下结论:①OA =OB;②△AOM≌△BON;③若∠AOB=45°,则S△AOB=k;④AB=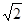 时,ON=BN=1,其中结论正确的是( )
时,ON=BN=1,其中结论正确的是( )
A. ①②③④ B. ①②③ C. ①② D. ①②④
A
试题分析:①②设A(x1,y1),B(x2,y2),联立
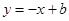 与
与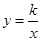 ,得x2-bx+k=0,则x1•x2=k,又x1•y1=k,比较可知x2=y1,同理可得x1=y2,即ON=OM,AM=BN,可证结论;
,得x2-bx+k=0,则x1•x2=k,又x1•y1=k,比较可知x2=y1,同理可得x1=y2,即ON=OM,AM=BN,可证结论;③作OH⊥AB,垂足为H,根据对称性可证△OAM≌△OAH≌△OBH≌△OBN,可证S△AOB=k;
④延长MA,NB交于G点,可证△ABG为等腰直角三角形,当AB=
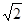 时,GA=GB=1,则ON-BN=GN-BN=GB=1.
时,GA=GB=1,则ON-BN=GN-BN=GB=1.A(x1,y1),B(x2,y2),代入
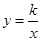 中,得x1•y1=x2•y2=k,
中,得x1•y1=x2•y2=k,联立
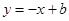 与
与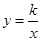 ,得x2-bx+k=0,
,得x2-bx+k=0,则x1•x2=k,又x1•y1=k,
∴x2=y1,
同理x2•y2=k,
可得x1=y2,
∴ON=OM,AM=BN,
∴①OA=OB,②△AOM≌△BON,正确;
③作OH⊥AB,垂足为H,
∵OA=OB,∠AOB=45°,
∵②△AOM≌△BON,正确;
∴∠MOA=∠BON=22.5°,
∠AOH=∠BOH=22.5°,
∴△OAM≌△OAH≌△OBH≌△OBN,
∴S△AOB=S△AOH+S△BOH=S△AOM+S△BON=
 k+
k+ k=k,正确;
k=k,正确;④延长MA,NB交于G点
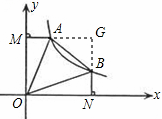
∵NG=OM=ON=MG,BN=AM,
∴GB=GA,
∴△ABG为等腰直角三角形,
当AB=
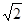 时,GA=GB=1,
时,GA=GB=1,∴ON-BN=GN-BN=GB=1,正确.
正确的结论有①②③④.
故选A.
点评:解题的关键是明确反比例函数图象上点的坐标特点,反比例函数图象的对称性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 、
、 在第一象限的图像,
在第一象限的图像, ,过
,过 ,作
,作 轴的平行线交
轴的平行线交 ,交
,交 轴于
轴于 ,若
,若 ;求双曲线
;求双曲线
 ,垂足为C,OA的垂直平分线交OC于B,且,则
,垂足为C,OA的垂直平分线交OC于B,且,则 的周长为( )
的周长为( )
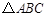 中,
中,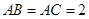 ,
,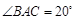 .
.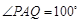 ,设
,设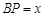 ,
,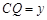 ,则
,则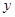 与
与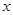 之间的函数关系式为 .
之间的函数关系式为 .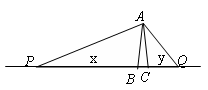
 的图象经过点(-2、5),则该函数的图象在平面直角坐标系中位于第 象限。
的图象经过点(-2、5),则该函数的图象在平面直角坐标系中位于第 象限。 是
是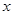 轴正半轴上的一个定点,点
轴正半轴上的一个定点,点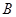 是双曲线
是双曲线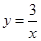 (
(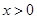 )上的一个动点,当点
)上的一个动点,当点 的面积将会( )
的面积将会( )
 、
、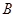 、
、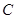 在双曲线
在双曲线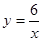 上,
上, 轴于
轴于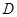 ,
, 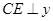 轴于
轴于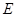 ,点
,点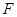 在
在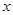 轴上,且
轴上,且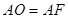 , 则图中阴影部分的面积之为 .
, 则图中阴影部分的面积之为 .