题目内容
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数 ![]() (k≠0)在第一象限内的图像经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图像经过点D、E,且tan∠BOA= ![]() .
.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图像与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
【答案】
(1)
解:∵点E(4,n)在边AB上,
∴OA=4,
在Rt△AOB中,∵tan∠BOA= ![]() ,
,
∴AB=OA×tan∠BOA=4× ![]() =2
=2
(2)
解:根据(1),可得点B的坐标为(4,2),
∵点D为OB的中点,
∴点D(2,1)
∴ ![]() =1,
=1,
解得k=2,
∴反比例函数解析式为y= ![]() ,
,
又∵点E(4,n)在反比例函数图像上,
∴ ![]() =n,
=n,
解得n= ![]()
(3)
解:如图,
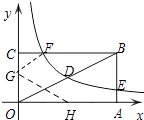
设点F(a,2),
∵反比例函数的图像与矩形的边BC交于点F,
∴ ![]() =2,
=2,
解得a=1,
∴CF=1,
连接FG,设OG=t,则OG=FG=t,CG=2﹣t,
在Rt△CGF中,GF2=CF2+CG2,
即t2=(2﹣t)2+12,
解得t= ![]() ,
,
∴OG=t= ![]() .
.
【解析】(1)根据点E的纵坐标判断出OA=4,再根据tan∠BOA= ![]() 即可求出AB的长度;(2)根据(1)求出点B的坐标,再根据点D是OB的中点求出点D的坐标,然后利用待定系数法求函数解析式求出反比例函数解析式,再把点E的坐标代入进行计算即可求出n的值;(3)先利用反比例函数解析式求出点F的坐标,从而得到CF的长度,连接FG,根据折叠的性质可得FG=OG,然后用OG表示出CG的长度,再利用勾股定理列式计算即可求出OG的长度.
即可求出AB的长度;(2)根据(1)求出点B的坐标,再根据点D是OB的中点求出点D的坐标,然后利用待定系数法求函数解析式求出反比例函数解析式,再把点E的坐标代入进行计算即可求出n的值;(3)先利用反比例函数解析式求出点F的坐标,从而得到CF的长度,连接FG,根据折叠的性质可得FG=OG,然后用OG表示出CG的长度,再利用勾股定理列式计算即可求出OG的长度.
【考点精析】本题主要考查了反比例函数的图象和反比例函数的性质的相关知识点,需要掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】某兴趣小组10名学生在一次数学测试中的成绩如表(满分150分)
分数(单位:分) | 105 | 130 | 140 | 150 |
人数(单位:人) | 2 | 4 | 3 | 1 |
下列说法中,不正确的是( )
A.这组数据的众数是130
B.这组数据的中位数是130
C.这组数据的平均数是130
D.这组数据的方差是112.5