Question

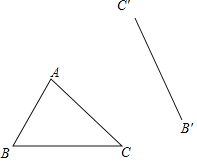
【题目】在平面直角坐标系中，将()沿直线运动到点，若点的坐标为，则称点为点的“铅直变换点”。

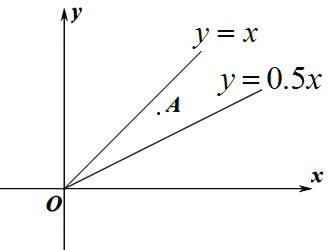
(1) 点的铅直变换点坐标___________；一个点的铅直变换点是，则这个点的坐标_________

(2) 已知点的坐标为(). 点在一次函数的图像上,点的铅直变换点为点，若这三个点中，其中的两个点关于另一点成中心对称，求的值.

(3) 已知点在一次函数和一次函数的图像所组成的角的内部，它的铅直变换点为点B，且满足，判断线段的长度能否等于，若能，求点的坐标，若不能，请说明理由。

Answer 1

【答案】(1) ， ；(2) ； (3) 不能

【解析】

（1）根据“铅直变换点”的定义即可求解；

（2）根据“铅直变换点”的定义写出B点坐标，再根据中心对称的特点分情况讨论；

（3）根据A点处于夹角内部得到＜b＜a,得到a-b＞0，B点坐标为（a,a-b），根据=a-b得到＜，求出a的取值，再得到b＞a-b，从而得到AB的长度，根据的长度为得到a,b之间的关系，再代入，根据根的判别式即可求解.

（1）点的铅直变换点坐标为（4,4-3），即为；

一个点的铅直变换点是，即，则这个点的坐标为；

故填： ，；

（2）∵点的坐标为(). 点在一次函数的图像上,

∴点（a,b+1），∴A的铅直变换点为点（a,1），

①若A,B关于C成中心对称，则

解得a=

②若C,B关于A成中心对称，则

解得a=3

③若A,C关于B成中心对称，则

解得a=

故时这三个点中，其中的两个点关于另一点成中心对称；

（3）不能，理由如下：

根据A点处于夹角内部得到＜b＜a,

∴a-b＞0，

∵A（a,b）

∴B点坐标为（a,a-b），

∵，

∴a-b=，

∵＜b

∴a-＜b

∴a-b＜

即＜

故a（2a-1）＜0，

根据二次函数图像可得a的取值为0＜a＜；

又＜b＜a,

∴b＞a-b，

故AB=b-（a-b）=2b-a=

得到b=

代入，得

△=16-4×8=-16＜0，

故a无解，即的长度不能等于.