题目内容
 如图,已知:△ABC内接于⊙O,AD是⊙O的切线,CO的延长线交AD于点D.
如图,已知:△ABC内接于⊙O,AD是⊙O的切线,CO的延长线交AD于点D.(1)若∠B=2∠D,求∠D的度数;
(2)在(1)的条件下,若AC=4
| 3 |
分析:(1)根据已知条件,利用弦切角定理和三角形内角和定理即可得出∠D的度数;
(2)根据切线与半径之间的位置关系,利用正切在直角三角形各边的数量关系,即可得出⊙O的半径.
(2)根据切线与半径之间的位置关系,利用正切在直角三角形各边的数量关系,即可得出⊙O的半径.
解答: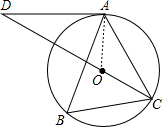 解:(1)如图,连接OA,
解:(1)如图,连接OA,
∵AD是⊙O的切线,
∴∠OAD=90°,
设∠D=α,则∠DOA=90°-α,∠B=2α,∠AOC=4α,
∴90°-α+4α=180°,
∴α=30°,
∴∠D=30°;
(2)∵OA=OC,∠AOC=4α=120°,
∴∠ACO=30°=∠D,
∴AD=AC=4
,
在Rt△ADO中,AO=AD×tan∠D=4
×
=4.
∴⊙O的半径是4.
 解:(1)如图,连接OA,
解:(1)如图,连接OA,∵AD是⊙O的切线,
∴∠OAD=90°,
设∠D=α,则∠DOA=90°-α,∠B=2α,∠AOC=4α,
∴90°-α+4α=180°,
∴α=30°,
∴∠D=30°;
(2)∵OA=OC,∠AOC=4α=120°,
∴∠ACO=30°=∠D,
∴AD=AC=4
| 3 |
在Rt△ADO中,AO=AD×tan∠D=4
| 3 |
| ||
| 3 |
∴⊙O的半径是4.
点评:本题主要考查了切线的性质和应用,要求学生能够熟练地应用切线的各个性质和定理.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
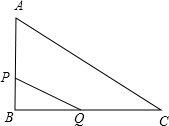
 如图,已知:△ABC中,∠1=∠2,且AE=AD,BE和CD相交于F.求证:BF=CF.
如图,已知:△ABC中,∠1=∠2,且AE=AD,BE和CD相交于F.求证:BF=CF. 如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE.
如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE. 如图,已知在△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线,则
如图,已知在△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线,则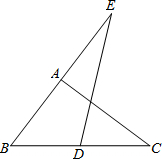 如图,已知在△ABC中,D是边BC的中点,点E在边BA的延长线上,AE=AB,
如图,已知在△ABC中,D是边BC的中点,点E在边BA的延长线上,AE=AB,