题目内容
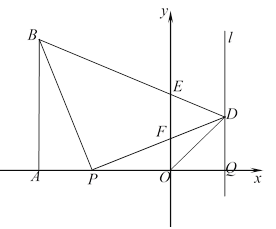
【题目】在四边形ABCD中,AB//DC,∠A=60°,AD=DC=BC=4,点E沿A→D→C→B运动,同时点F沿A→B→C运动,运动速度均为每秒1个单位,当两点相遇时,运动停止.则△AEF的面积y与运动时间x秒之间的图象大致为( )
A.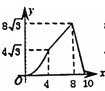 B.
B.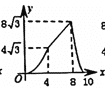 C.
C.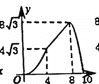 D.
D.
【答案】A
【解析】
分点E在AD上、点E在DC上, 点E在BC上运动时三种情况,分别求出函数表达式,进而求解.
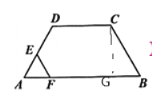
解:当0![]() x<4时,AE=AF=x,∠A=60°,∴三角形AEF是等边三角形.∴y=
x<4时,AE=AF=x,∠A=60°,∴三角形AEF是等边三角形.∴y=![]() x2.
x2.
当4![]() x<8时,点E在DC上,点F在AB上,AF=x,过点C作CG⊥AB,在Rt
x<8时,点E在DC上,点F在AB上,AF=x,过点C作CG⊥AB,在Rt![]() BCG中,∠B=60°,BC=4,则BG=2,CG=2
BCG中,∠B=60°,BC=4,则BG=2,CG=2![]() .∴y=
.∴y=![]() x
x![]() 2
2![]() =
=![]()
当8![]() x<10时,E,F均在BC上,则BE=12-x.BF=x-8,则E到AB的高为6
x<10时,E,F均在BC上,则BE=12-x.BF=x-8,则E到AB的高为6![]() -
-![]() x,点F到AB的高为
x,点F到AB的高为![]() x-4
x-4![]() .∴y=
.∴y=![]() 8[(6
8[(6![]() -
-![]() x)-(
x)-(![]() x-4
x-4![]() )]=-4
)]=-4![]() .故选A.
.故选A.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案【题目】王老师从本校九年级质量检测的成绩中随机地抽取一些同学的数学成绩做质量分析,他先按照等级绘制这些人数学成绩的扇形统计图,如图(1)所示,数学成绩等级标准见表1,又按分数段绘制成绩分布表,如表2,
表1
等级 | 分数x的范围 |
A | a≤x≤100 |
B | 80≤x<a |
C | 60≤x<80 |
D | 0≤x<60 |
表2
分数段 | x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
人数 | 5 | 10 | m | 12 | n |
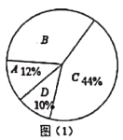
分数段为90≤x≤100的n个人中,其成绩的中位数是95分.
根据以上信息回答下面问题:
(1)王老师抽查了多少人?m、n的值分别是多少;
(2)小明在此考试中得了95分,他说自己在这些考试中数学成绩是A等级,他说的对吗?为什么?
(3)若此次测试数学学科普高的预测线是70分,该校九年级有900名学生,求数学学科达到普高预测线的学生约有多少人?
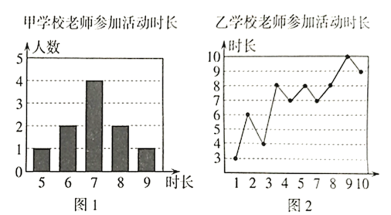
【题目】甲、乙两所学校选派相同人数的老师参加志愿者活动,參加活动时长分别被制成下列两个统计图,根据以上信息,整理分析数据如下表:
平均时间/小时 | 中位数/小时 | 众数/小时 | 方差/小时 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
![]() 求出表格中
求出表格中![]() 的值.
的值.
![]() 分别运用表中的统计量,简要分析这两所学校参加志愿者活动的时长,若选其中一所学校作为志愿推广学校,你认为应该选哪所?
分别运用表中的统计量,简要分析这两所学校参加志愿者活动的时长,若选其中一所学校作为志愿推广学校,你认为应该选哪所?
【题目】研究机构对本地区18-20岁的大学生就某个问题做随机调查,要求被调查者从A、B、C、D四个选项中选择自己赞同的一项,并将结果绘制成两幅不完整的统计图(如图):
大学生就某个问题调查结果统计表 | 大学生就某个问题调查结果扇形统计图 | ||||||||||||
|
|
请结合图中信息解答以下问题:
(1)m=_____,b=_____.
(2)若该地区18~20岁的大学生有1.2万人,请估计这些大学生中选择赞同A选项的人数:
(3)该研究机构决定从选择“C”的人中随机抽取2名进行访谈,而选择“C”的这4人中只有一名男性,求这名男性刚好被抽取到的概率.