题目内容
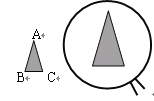
【题目】定义:如图![]() ,若点D在
,若点D在![]() 的边AB上,且满足
的边AB上,且满足![]() ,则称满足这样条件的点为
,则称满足这样条件的点为![]() 的“理想点”
的“理想点”
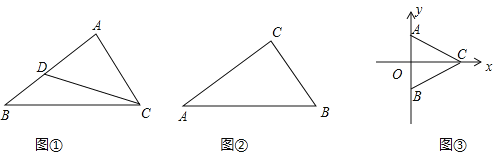
![]() 如图
如图![]() ,若点D是
,若点D是![]() 的边AB的中点,
的边AB的中点,![]() ,
,![]() ,试判断点D是不是
,试判断点D是不是![]() 的“理想点”,并说明理由;
的“理想点”,并说明理由;
![]() 如图
如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点D是
,若点D是![]() 的“理想点”,求CD的长;
的“理想点”,求CD的长;
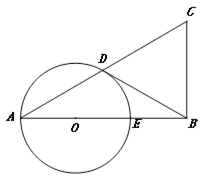
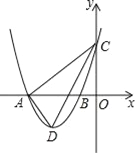
![]() 如图,已知平面直角坐标系中,点
如图,已知平面直角坐标系中,点![]() ,
,![]() ,C为x轴正半轴上一点,且满足
,C为x轴正半轴上一点,且满足![]() ,在y轴上是否存在一点D,使点A,B,C,D中的某一点是其余三点围成的三角形的“理想点”
,在y轴上是否存在一点D,使点A,B,C,D中的某一点是其余三点围成的三角形的“理想点”![]() 若存在,请求出点D的坐标;若不存在,请说明理由.
若存在,请求出点D的坐标;若不存在,请说明理由.
【答案】![]() 见解析;(2)
见解析;(2)![]() ;(3)存在,理由见解析.
;(3)存在,理由见解析.
【解析】
![]() 结论:点D是
结论:点D是![]() 的“理想点”
的“理想点”![]() 只要证明
只要证明![]() ∽
∽![]() 即可解决问题;
即可解决问题;
![]() 只要证明
只要证明![]() 即可解决问题;
即可解决问题;
![]() 如图
如图![]() 中,存在
中,存在![]() 有三种情形:过点A作
有三种情形:过点A作![]() 交CB的延长线于M,作
交CB的延长线于M,作![]() 轴于
轴于![]() 构造全等三角形,利用平行线分线段成比例定理构建方程求出点C坐标,分三种情形求解即可解决问题;
构造全等三角形,利用平行线分线段成比例定理构建方程求出点C坐标,分三种情形求解即可解决问题;
解:![]() 结论:点D是
结论:点D是![]() 的“理想点”.
的“理想点”.
理由:如图![]() 中,
中,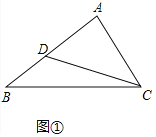
![]() 是AB中点,
是AB中点,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ∽
∽![]() ,
,![]() ,
,![]() 点D是
点D是![]() 的“理想点”,
的“理想点”,![]() 如图
如图![]() 中,
中,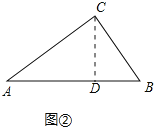
![]() 点D是
点D是![]() 的“理想点”,
的“理想点”,![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
当![]() 时,同法证明:
时,同法证明:![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() 如图
如图![]() 中,存在
中,存在![]() 有三种情形:
有三种情形: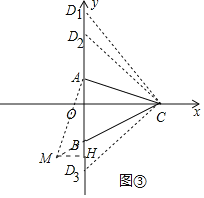
过点A作![]() 交CB的延长线于M,作
交CB的延长线于M,作![]() 轴于H.
轴于H.![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ≌
≌![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
解得![]() 或
或![]() 舍弃
舍弃![]() ,
,
经检验![]() 是分式方程的解,
是分式方程的解,![]() ,
,![]() ,
,![]() 当
当![]() 时,点A是
时,点A是![]() 的“理想点”
的“理想点”![]() 设
设![]() ,
,![]() ,
,![]() ,
,![]() ∽
∽![]() ,
,![]() ,
,![]() ,
,
解得![]() ,
,![]() .
.![]() 当
当![]() 时,点A是
时,点A是![]() 的“理想点”.
的“理想点”.
易知:![]() ,
,![]() ,
,![]() .
.![]() 当
当![]() 时,点B是
时,点B是![]() 的“理想点”.
的“理想点”.
易知:![]() ,
,![]() ,
,![]() .
.
综上所述,满足条件的点D坐标为![]() 或
或![]() 或
或![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.