题目内容
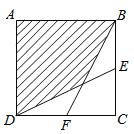
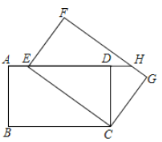
【题目】如图,将矩形ABCD绕点C旋转得到矩形EFGC,点E在AD上.延长AD交FG于点H
(1)求证:△EDC≌△HFE;
(2)若∠BCE=60°,连接BE、CH.证明:四边形BEHC是菱形.
【答案】(1)见解析;(2)见解析.
【解析】
(1)依据题意可得到FE=AB=DC,∠F=∠EDC=90°,FH∥EC,利用平行线的性质可证明∠FHE=∠CED,然后依据AAS证明△EDC≌△HFE即可;
(2)首先证明四边形BEHC为平行四边形,再证明邻边BE=BC即可证明四边形BEHC是菱形.
(1)证明:∵矩形FECG由矩形ABCD旋转得到,
∴FE=AB=DC,∠F=∠EDC=90°,FH∥EC,
∴∠FHE=∠CED.
在△EDC和△HFE中,
 ,
,
∴△EDC≌△HFE(AAS);
(2)∵△EDC≌△HFE,
∴EH=EC.
∵矩形FECG由矩形ABCD旋转得到,
∴EH=EC=BC,EH∥BC,
∴四边形BEHC为平行四边形.
∵∠BCE=60°,EC=BC,
∴△BCE是等边三角形,
∴BE=BC,
∴四边形BEHC是菱形.

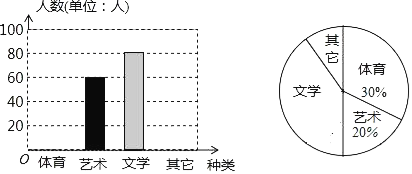
【题目】小夏同学从家到学校有![]() ,
,![]() 两条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
两条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时 频数 公交车路线 |
|
|
|
| 总计 |
| 59 | 151 | 166 | 124 | 500 |
| 43 | 57 | 149 | 251 | 500 |
据此估计,早高峰期间,乘坐![]() 线路“用时不超过35分钟”的概率为__________,若要在40分钟之内到达学校,应尽量选择乘坐__________(填
线路“用时不超过35分钟”的概率为__________,若要在40分钟之内到达学校,应尽量选择乘坐__________(填![]() 或
或![]() )线路.
)线路.
【题目】阅读下面内容,并按要求解决问题:
问题:“在平面内,已知分别有2个点,3个点,4个点,5个点,…,![]() 个点,其中任意三个点都不在同一条直线上经过每两点画一条直线,它们可以分别画多少条直线?”
个点,其中任意三个点都不在同一条直线上经过每两点画一条直线,它们可以分别画多少条直线?”
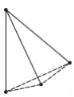
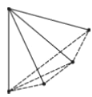
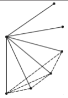
探究:为了解决这个问题,希望小组的同学们,设计了如下表格进行探究:(为了方便研究问题,图中每条线段表示过线段两端点的一条直线)
点数 | 2 | 3 | 4 | 5 | … |
|
示意图 |
|
|
|
| … |
|
直线条数 | 1 |
|
|
| … |
请解答下列问题:
(1)请帮助希望小组归纳,并直接写出结论:当平面内有个点时,直线条数为______;
(2)若某同学按照本题中的方法,共画了28条直线,求该平面内有多少个已知点?