题目内容
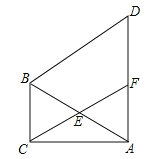
【题目】如图,CD是△ABC的中线,点E、F分别是AC、DC的中点,EF=1,则BD= . 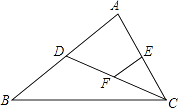
【答案】2
【解析】解:∵点E、F分别是AC、DC的中点,
∴EF是△ADC的中位线,
∴EF= ![]() AD,
AD,
∵EF=1,
∴AD=2,
∵CD是△ABC的中线,
∴BD=AD=2,
所以答案是:2.
【考点精析】解答此题的关键在于理解三角形的“三线”的相关知识,掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内,以及对三角形中位线定理的理解,了解连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.

【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0.365 | 0.328 | 0.330 | 0.334 | 0.336 | 0.332 | 0.333 |
则符合这一结果的实验最有可能的是( )
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是梅花
B.抛一枚硬币,出现反面的概率
C.袋子里有除了颜色都一样3个红球,2个白球,随机摸一个球是白球的概率
D.抛一个质地均匀的正六面体骰子,向上的面点数大于4
【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?