题目内容
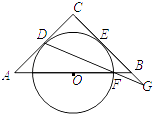
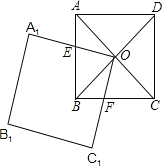
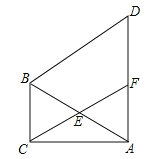
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)若AB=6,求平行四边形BCFD的面积.
【答案】(1)证明见解析;(2)9![]() .
.
【解析】
(1)在Rt△ABC 中,E为AB的中点,则CE![]() AB,BE
AB,BE![]() AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°,又∠D=60°,得∠AFE=∠D=60°,所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD∥BC,由此即可得四边形BCFD是平行四边形;
AB,得到∠BCE=∠EBC=60°.由△AEF≌△BEC,得∠AFE=∠BCE=60°,又∠D=60°,得∠AFE=∠D=60°,所以FC∥BD,又因为∠BAD=∠ABC=60°,所以AD∥BC,即FD∥BC,由此即可得四边形BCFD是平行四边形;
(2)在Rt△ABC中,求出BC,AC即可解决问题.
(1)在△ABC中,∠ACB=90°,∠CAB=30°,
∴∠ABC=60°,
在等边△ABD中,∠BAD=60°,∴∠BAD=∠ABC=60°,
∵E为AB的中点,∴AE=BE,
又∵∠AEF=∠BEC,∴△AEF≌△BEC,
在△ABC中,∠ACB=90°,E为AB的中点,
∴CE![]() AB,BE
AB,BE![]() AB,
AB,
∴CE=AE,
∴∠EAC=∠ECA=30°,∴∠BCE=∠EBC=60°,
又∵△AEF≌△BEC,∴∠AFE=∠BCE=60°,
又∵∠D=60°,∴∠AFE=∠D=60°,∴FC∥BD,
又∵∠BAD=∠ABC=60°,∴AD∥BC,即FD∥BC,
∴四边形BCFD是平行四边形;
(2)在Rt△ABC中,∵∠BAC=30°,AB=6,
∴BC![]() AB=3,AC=
AB=3,AC=![]() =3
=3![]() ,
,
∴S平行四边形BCFD=3![]() .
.

练习册系列答案
相关题目