جâؤ؟ؤعبف
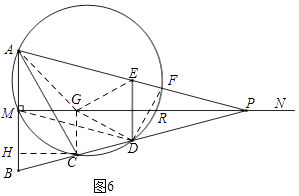
،¾جâؤ؟،؟بçح¼£¬زرضھدك¶خAB=2£¬MN،حABسعµمM£¬ازAM=BM£¬PتاةندكMNةدز»¶¯µم£¬E£¬D·ض±ًتاPA£¬PBµؤضذµم£¬¹µمA£¬M£¬Dµؤش²سëBPµؤءيز»½»µمC£¨µمCشعدك¶خBDةد£©£¬ء¬½لAC£¬DE£®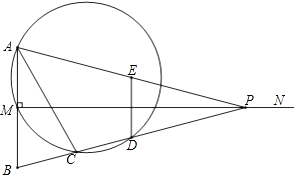
£¨1£©µ±،دAPB=28،مت±£¬اَ،دB؛ح ![]() µؤ¶بت£»
µؤ¶بت£»
£¨2£©اَض¤£؛AC=AB£®
£¨3£©شعµمPµؤشث¶¯¹³جضذ
¢ظµ±MP=4ت±£¬ب،ثؤ±كذخACDEز»±كµؤء½¶ثµم؛حدك¶خMPةدز»µمQ£¬بôزشصâبµمخھ¶¥µمµؤب½اذختاض±½اب½اذخ£¬ازQخھبٌ½ا¶¥µم£¬اَثùسذآْ×مجُ¼µؤMQµؤضµ£»
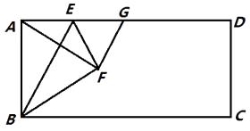
¢ع¼اAPسëش²µؤءيز»¸ِ½»µمخھF£¬½«µمFبئµمDذ×ھ90،مµأµ½µمG£¬µ±µمGا،؛أآنشعMNةدت±£¬ء¬½لAG£¬CG£¬DG£¬EG£¬ض±½سذ´³ِ،÷ACG؛ح،÷DEGµؤأو»ض®±ب£®
،¾´ً°¸،؟
£¨1£©
½â£؛،كMN،حAB£¬AM=BM£¬
،àPA=PB£¬
،à،دPAB=،دB£¬
،ك،دAPB=28،م£¬
،à،دB=76،م£¬
بçح¼1£¬ء¬½سMD£¬
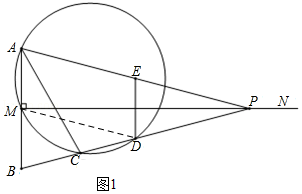
،كMDخھ،÷PABµؤضذخ»دك£¬
،àMD،خAP£¬
،à،دMDB=،دAPB=28،م£¬
،à ![]() =2،دMDB=56،م£»
=2،دMDB=56،م£»
£¨2£©
ض¤أ÷£؛،ك،دBAC=،دMDC=،دAPB£¬
سض،ك،دBAP=180،م©پ،دAPB©پ،دB£¬،دACB=180،م©پ،دBAC©پ،دB£¬
،à،دBAP=،دACB£¬
،ك،دBAP=،دB£¬
،à،دACB=،دB£¬
،àAC=AB£»
£¨3£©
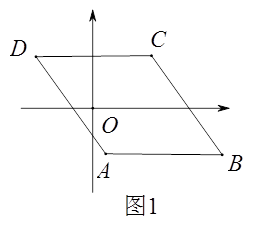
½â£؛¢ظبçح¼2£¬¼اMPسëش²µؤءيز»¸ِ½»µمخھR£¬

،كMDتاRt،÷MBPµؤضذدك£¬
،àDM=DP£¬
،à،دDPM=،دDMP=،دRCD£¬
،àRC=RP£¬
،ك،دACR=،دAMR=90،م£¬
،àAM2+MR2=AR2=AC2+CR2£¬
،à12+MR2=22+PR2£¬
،à12+£¨4©پPR£©2=22+PR2£¬
،àPR= ![]() £¬
£¬
،àMR= ![]() £¬
£¬
¢ٌ£®µ±،دACQ=90،مت±£¬AQخھش²µؤض±¾¶£¬
،àQسëRضط؛د£¬
،àMQ=MR= ![]() £»
£»
¢ٍ£®بçح¼3£¬µ±،دQCD=90،مت±£¬
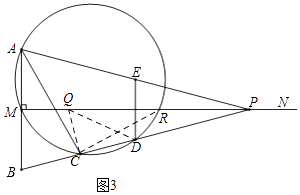
شعRt،÷QCPضذ£¬PQ=2PR= ![]() £¬
£¬
،àMQ= ![]() £»
£»
¢َ£®بçح¼4£¬µ±،دQDC=90،مت±£¬
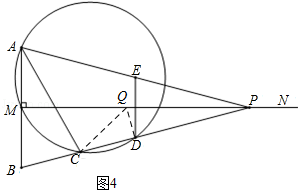
،كBM=1£¬MP=4£¬
،àBP= ![]() £¬
£¬
،àDP= ![]() BP=
BP= ![]() £¬
£¬
،كcos،دMPB= ![]() =
= ![]() £¬
£¬
،àPQ= ![]() £¬
£¬
،àMQ= ![]() £»
£»
¢ô£®بçح¼5£¬µ±،دAEQ=90،مت±£¬
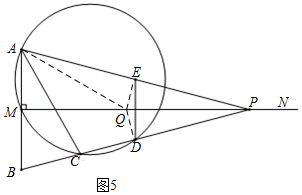
سة¶ش³ئذش؟ةµأ،دAEQ=،دBDQ=90،م£¬
،àMQ= ![]() £»
£»
×غةدثùتِ£¬MQµؤضµخھ ![]() »ٍ
»ٍ ![]() »ٍ
»ٍ ![]() £»
£»
¢ع،÷ACG؛ح،÷DEGµؤأو»ض®±بخھ ![]() £®
£®
ہيسة£؛بçح¼6£¬،كDM،خAF£¬
،àDF=AM=DE=1£¬
سضسة¶ش³ئذش؟ةµأGE=GD£¬
،à،÷DEGتاµب±كب½اذخ£¬
،à،دEDF=90،م©پ60،م=30،م£¬
،à،دDEF=75،م=،دMDE£¬
،à،دGDM=75،م©پ60،م=15،م£¬
،à،دGMD=،دPGD©پ،دGDM=15،م£¬
،àGMD=،دGDM£¬
،àGM=GD=1£¬
¹C×÷CH،حABسعH£¬
سة،دBAC=30،م؟ةµأCH= ![]() AC=
AC= ![]() AB=1=MG£¬AH=
AB=1=MG£¬AH= ![]() £¬
£¬
،àCG=MH= ![]() ©پ1£¬
©پ1£¬
،àS،÷ACG= ![]() CG،ءCH=
CG،ءCH= ![]() £¬
£¬
،كS،÷DEG= ![]() £¬
£¬
،àS،÷ACG£؛S،÷DEG= ![]() £®
£®
،¾½âخِ،؟£¨1£©¸ù¾فب½اذخABPتاµبرüب½اذخ£¬؟ةµأ،دBµؤ¶بت£¬شظء¬½سMD£¬¸ù¾فMDخھ،÷PABµؤضذخ»دك£¬؟ةµأ،دMDB=،دAPB=28،م£¬½ّ¶ّµأµ½ ![]() =2،دMDB=56،م£»£¨2£©¸ù¾ف،دBAP=،دACB£¬،دBAP=،دB£¬¼´؟ةµأµ½،دACB=،دB£¬½ّ¶ّµأ³ِAC=AB£»£¨3£©¢ظ¼اMPسëش²µؤءيز»¸ِ½»µمخھR£¬¸ù¾فAM2+MR2=AR2=AC2+CR2 £¬ ¼´؟ةµأµ½PR=
=2،دMDB=56،م£»£¨2£©¸ù¾ف،دBAP=،دACB£¬،دBAP=،دB£¬¼´؟ةµأµ½،دACB=،دB£¬½ّ¶ّµأ³ِAC=AB£»£¨3£©¢ظ¼اMPسëش²µؤءيز»¸ِ½»µمخھR£¬¸ù¾فAM2+MR2=AR2=AC2+CR2 £¬ ¼´؟ةµأµ½PR= ![]() £¬MR=
£¬MR= ![]() £¬شظ¸ù¾فQخھض±½اب½اذخبٌ½ا¶¥µم£¬·ضثؤضضاé؟ِ½ّذذجضآغ£؛µ±،دACQ=90،مت±£¬µ±،دQCD=90،مت±£¬µ±،دQDC=90،مت±£¬µ±،دAEQ=90،مت±£¬¼´؟ةاَµأMQµؤضµخھ
£¬شظ¸ù¾فQخھض±½اب½اذخبٌ½ا¶¥µم£¬·ضثؤضضاé؟ِ½ّذذجضآغ£؛µ±،دACQ=90،مت±£¬µ±،دQCD=90،مت±£¬µ±،دQDC=90،مت±£¬µ±،دAEQ=90،مت±£¬¼´؟ةاَµأMQµؤضµخھ ![]() »ٍ
»ٍ ![]() »ٍ
»ٍ ![]() £»¢عدبإذ¶¨،÷DEGتاµب±كب½اذخ£¬شظ¸ù¾فGMD=،دGDM£¬µأµ½GM=GD=1£¬¹C×÷CH،حABسعH£¬سة،دBAC=30،م؟ةµأCH=
£»¢عدبإذ¶¨،÷DEGتاµب±كب½اذخ£¬شظ¸ù¾فGMD=،دGDM£¬µأµ½GM=GD=1£¬¹C×÷CH،حABسعH£¬سة،دBAC=30،م؟ةµأCH= ![]() AC=1=MG£¬¼´؟ةµأµ½CG=MH=
AC=1=MG£¬¼´؟ةµأµ½CG=MH= ![]() ©پ1£¬½ّ¶ّµأ³ِS،÷ACG=
©پ1£¬½ّ¶ّµأ³ِS،÷ACG= ![]() CG،ءCH=
CG،ءCH= ![]() £¬شظ¸ù¾فS،÷DEG=
£¬شظ¸ù¾فS،÷DEG= ![]() £¬¼´؟ةµأµ½،÷ACG؛ح،÷DEGµؤأو»ض®±ب£®
£¬¼´؟ةµأµ½،÷ACG؛ح،÷DEGµؤأو»ض®±ب£®

،¾جâؤ؟،؟خز¹ْدضذذµؤ¶´ْةي·فض¤؛إآëتا18خ»ت×ض£¬سةا°17خ»ت×ض±¾جهآë؛ح×î؛َ1خ»ذ£رéآë×é³ة.ذ£رéآëح¨¹ا°17خ»ت×ض¸ù¾فز»¶¨¹وشٍ¼ئثمµأ³ِ£¬بç¹ûذ£رéآë²»·û؛دصâ¸ِ¹وشٍ£¬ؤاأ´¸أ؛إآë؟د¶¨تا¼ظ؛إآë.دض½«ا°17خ»ت×ض±¾جهآë¼اخھ![]() £¬ئنضذ
£¬ئنضذ![]() ±يت¾µع
±يت¾µع![]() خ»ضأةدµؤةي·فض¤؛إآëت×ضضµ£¬°´دآ±يضذµؤ¹و¶¨·ض±ً¸ّ³ِأ؟¸ِخ»ضأةدµؤز»¸ِ¶شس¦µؤضµ
خ»ضأةدµؤةي·فض¤؛إآëت×ضضµ£¬°´دآ±يضذµؤ¹و¶¨·ض±ً¸ّ³ِأ؟¸ِخ»ضأةدµؤز»¸ِ¶شس¦µؤضµ![]() .
.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 7 | 9 | 10 | 5 | 8 | 4 | 2 | 1 | 6 | 3 | 7 | 9 | 10 | 5 | 8 | 4 | 2 |
| 4 | 4 | 0 | 5 | 2 | 4 | 1 | 9 | 8 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
دضزش؛إآë![]() خھہ£¬دب½«¸أ؛إآë
خھہ£¬دب½«¸أ؛إآë![]() µؤا°17خ»ت×ض±¾جهآëجîبë±يضذ(دضزرجî؛أ)£¬زہصصزشدآ²ظ×÷²½ضè¼ئثمدàس¦µؤذ£رéآë½ّذذذ£رé:
µؤا°17خ»ت×ض±¾جهآëجîبë±يضذ(دضزرجî؛أ)£¬زہصصزشدآ²ظ×÷²½ضè¼ئثمدàس¦µؤذ£رéآë½ّذذذ£رé:
£¨1£©¶شا°17خ»ت×ض±¾جهآ룬°´دآءذ·½ت½اَ؛ح£¬²¢½«؛ح¼اخھ![]() £؛
£؛
![]() .
.
دض¾¼ئثم£¬زرµأ³ِ![]() £¬¼جذّاَµأ
£¬¼جذّاَµأ![]() ____£»
____£»
£¨2£©¼ئثم![]() £¬ثùµأµؤسàت¼اخھ
£¬ثùµأµؤسàت¼اخھ![]() £¬ؤاأ´
£¬ؤاأ´![]() ____£»
____£»
£¨3£©²éشؤدآ±يµأµ½¶شس¦µؤذ£رéآ루ئنضذ![]() خھآقآيت×ض£¬سأہ´´ْجو10£©£؛
خھآقآيت×ض£¬سأہ´´ْجو10£©£؛
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
ذ£رéآë | 1 | 0 |
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 |
ثùµأµ½µؤذ£رéآëخھ____£¬سë؛إآë![]() ضذµؤ×î؛َز»خ»½ّذذ¶ش±ب£¬سة´ثإذ¶د؛إآë
ضذµؤ×î؛َز»خ»½ّذذ¶ش±ب£¬سة´ثإذ¶د؛إآë![]() تا____£¨جî،°صو،±»ٍ،°¼ظ،±£©ةي·فض¤؛إ.
تا____£¨جî،°صو،±»ٍ،°¼ظ،±£©ةي·فض¤؛إ.